получаем значение модуля результирующей частотной передаточной функции

\У0-(0) =Л((0) = Д,((0) (6.44)

и фазы

V((0) = - (ОТ.

(6.45)

Рис. 6.25

Таким образом, наличие звена с запаздыванием не меняет модуля и вносит только дополнительный фазовый сдвиг.

На рис. 6.25 изображена амнлитудно-(})а.зо-вая характеристика, соответствующая (6.43). Силопиюй линией показана исходная характеристика при т = О, а пунктиром - характеристика, которая получается при наличии постоянного запаздывания т/0.

Из этих характеристик видно, что наличие допол1И1тельиого фазового сдвига Д\/ = (ОТ закручивает годограф, особенно в высокочастотной части, но часовой стрелке. Это, вообще говоря, ухудннхет условия устойчивости, так как вся кривая приближается к точке (-1, jO). Иногда в особых случаях при сюжной (1)орме годографа WoOco), введение постоя1Н1ого запаздывания может улучшить условия устойчивости.

По имеющемуся годогра(})у ИоОй) можно определить критическое значение времени запаздывания т = тр, при котором система оказывается на границе колебательной устойчивости.

Для этой цели па годографе WqC/co) отыскивается точка, для которой модуль равен единице (рис. 6.25). Частоту, соответствующую этой точке, обозначим (о а фа,зу - Vi, При введении постоянного запа.здывапия т = тр условие совпадения этой точки с точкой (-1,70) запишется следуюнщм образом:

откуда критическое значение запа.здывапия

71 + V,

(6.46)

Если подобных опасных точек будет несколько, то необходимо сделать расчеты для всех точек и взять наименьшее значение тр.

Замети.м, что частота со, равна частоте среза л. а. х., со, = сор (см., напри.мер, рис. 6.18). Поэтому нахождение со, и Ц!, удобно делать при наличии ностроеппых л. а. x. и л. ф. x.

Л. а. x. системы с запаздыванием совпадает с л. а. х. исходной системы (без запаздывания). Дополнительный фазовый сдвиг, который надо учесть при построении л. ф. x. системы с запа.здыванием, определяехя (6.45).

В некоторых случаях .могут использоваться аналитические расчеты. Так, например, рассмотрим статическую систему с одной ностоя1июй времени. Частотная передаточная функция разо.мкнутой систе.мы имеет вид

Wo(j(o) = --. (6.47)

1-1- jcor

0,8 0,6 0,4 0,2

о 2 4 6 8 10 12 14 *

Рис, 6,26

Приравняем модуль единице: К

:=1.

Отсюда находится частота, соответствующая опасной точке:

(О, =-

Фазовый сдвиг на этой частоте

\;, = -arctg(o,r = -arctg/К -1. По формуле (6.46) находим критическое запаздывание:

1у1к-1 ,n-arctg>/K2-l

7i-arctgVA -1 n-arctg>

(6.48)

1

По этому выражению па рис. 6.26 построена область устойчивости в координатах общий коэффициент усиления - относительное запаздывание .

§ 6.7. Устойчивость систем

с распределенными параметрами

Системой авто.матнческого управления с распределенными параметрами называется такая система, среди уравнений которой кроме обыкновенных дифференциальных уравнений имеются уравнения в частных производных. Физически это соответствует учету волновых яв;1епий или гидравлического удара в трубопроводах, учету волновых процессов в длинных электрических линиях прн передаче по ни.м воздействий от одного звена системы автоматического управления к друго.му или же при управлении процессами в самих трубопроводах или длинных линиях.

Этот вопрос приобретает практическое значение чаще всего в некоторых системах управления, включающих в себя водяные, масляные или газовые трубопроводы (либо в объекте, либо в управляющем устройстве), реже - в некоторых системах телерегулирования (телеуправления)и т. и.

Известно, тгапри.мер, что водяной трубопровод гидротурбины описывается без учета потерь уравнениями

dh dh dv dt g дх

где V - скорость движения воды; - напор в произвольной точке, определяемой координатой X вдоль трубопровода; а - скорость звука в воде.

Уравнения длинной электрической линии без потерь имеют вид;

di ди дх dt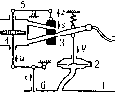

Подача

-/(О

=-ТГ

к потребитсгям

Рис. 6.27

где и - напряжение; г - ток в произвольной точке, определяемой координатой х вдоль линии; / и с - индуктивность и емкость единицы длины линии.

После ренгения указанных уравпепий в частных производных с учетом граничных условий, определяемых смсжпы.мп звеиья\и1 даппой системы автоматического управления, для системы в целом получаются уравпепия того же типа, как и для систем с запа:дываиием (§ 6.7).

Рассмотри.м вывод уравпепий системы стгюилизацип давления i-аза в трубопроводе, схема которой изображена tra рис. 6.27. В данном случае са.м объект (трубопровод) является звеном с распределенными параметрами. Для простоты будем считать его прямолинейным, а всех потребителей - сосредогочсрщыми па конце трубопровода.

Управляющее устройство состоит из чувствительного элемента 2 (мембранный измеритель давления), усилителей Зп4 (струящая трубка и пневматический двигатель) с жесткой обратной связью 5 и из управляющего органа 6 (клапан), Воз.муща-ющее во.здействие f{t) на объект выражается в изменении но произволу потребителей некоторого эквивалентпоге) выход1гого сечения на ко1гце трубопровода.

Уравнение управляемого объекта. Движение газа в трубопроводе подчиняется уравнению

dw dw 1 dp

- + w------.

dt dl p dl

Учтем также условия постоянства массы

Эр dw Эр -+ р--I- ;-= 0 dt dl dl

и адиабатическое уравнение состояния газа

.,0

(6.49)

(6.50)

(6.51)

В этих уравне1Шях w, р, р - соответственно скорость, давление и плотность газа в текущем сечении трубопровода с координатой / в момент времени г (вся длина трубопровода обозначается через L); k - показатель степени в уравнении адиабатичес-

кого состояния газа; индексы О вверху (р , р ) означают, что данные величины отно сятся к установившемуся состоянию системы.