где Wijii) - сшпчитудно-фюовая частотная характеристика линейной части системы. При наличии 0ЛИ01-0 нулевого полюса требуется enie, чтобы

Im W(/a)) ->-о° при со-> О,

а при двух нулевых полюсах

Re W (/О)) ->при а)->(), а lmWijw)<0 при малых со.

Теорема справедлива также и при наличии взпамеиателе Q(p) ие1)едаточной функпии линейной части не более двух чисто мни.мых корней, по при этом требуются некоторые другие простые добавочные условия [2], называемые условиями предельной устойчивости.

Другая формулировка той же теоре.\п>1, дающая удобную графическую интерп1)е-raiHiro, связана с введением видоизмененной частотной характеристики (joi), которая оп1)еделяется следующи.м образом:

и * (W) = RcW* (joi) = Re W(j(a), V * (со) = Im W * = coTq Im W(;co),

(17.85)

где Tq = 1 с - нормирующий .множитель.

График W* (jw) и.меет вид (рис. 17.16, а), 1Юхожий на W(jw), когда при отсутствии в W(j)) нулевых полюсов в вы1)ал<епиях Q(p)nR(р) раз1юстьстепеней п - m > 1. Если же разность степепей п - т= 1, то конец грас{)пка W* (/со) будет па \\\шио\\ оси ниже начала координат (рис. 17.16, б).

Преобразуем левую часть п(фавенства( 17.84):

+ - = RcW{jio) - со/г Im\V{jw) + -

Re(l-b;aj/z)lV(jaj) Тогда, положив

U*(;co) = (/*(co)+;T*(co)

и использовав соотношения (17.85), получим вместо (17.84) для теоремы В. М. По1Ю-ва условие

t/* (со) - * ( )+1 = * (со) - AoF * (со) +-1 > О

(17.86)

при п-т>\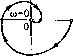

при всех со > 0.

Очевидно, что равенство

[/*(co)-/2oV*(co) + - = 0 (17.87)

представляет уравнение пря.мой иа плоскости W* (jw).

Отсюда вытекает следующая графическая интерпретация теоре.мы В. М. Попова: djm установления устойчивости не-

линейной системы, достаточно подобрать такую прямую на плоскости W* (jui), проходящую через точку

1 i

~-,jO , чтобы, вся кривая W* Цт)лежала справа от

kj: J

этой прямой.

Ла рис. 17,17 показаны случаи выполнения теоремы. В зтих случаях нелинейная система устойчива при любой фор.ме однозначной нелинейности, ограниченной лишь условием (17,83). На рис. 17.18 показаны случаи, когда теорема не выполнятся, т, е. нелинейная система не имеет абсолютной устойчивости.

Заметим, что, например, в задаче о самолете с авто-[нттото.м (§ 17.2) условие (17.,54) означает любое расположение нелинейной характеристики во всем нервом (и тре гье.м) квадранте. Во всех подобных случаях согласно рис. 17.1,5 имеем k = °o.B теореме В.М. Попова при это.м в.место (17.84) получаем условие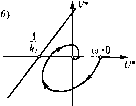

Рис. 17.17

Re(l + ;ш/г)и/(;со)>0.

(17.88)

а вместо (17.86)

Г/*(ш)-/гоУ*(со)>0

(17.89)

при всех со > 0. Поэто.му в гра({)ической интерпретации прякшя должна проходить не так, как показано на рис. 17.17, а через начало координат.

В частности, для указанного примера (§ 17.2) уравнепня (17,63) можно преобразовать к виду

у-fix.,), (1 + р)р% = [ф + (1+г)р+ у]у,

где обозначено г/ = -рХ2, причем/; - производная пот. Передаточная функция линейной части системы будет

р О + р)

Отсюда

-ю(1н- усо)

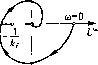Умножив числитель и знаменатель иа 1 -jio, получим

ReW(;ft))v

у + м

а согласно (17.85)

-(о(1 + м)

-, IniW(;M) =

(1 + г-у)ы + га)- -м\1 + (0)

У + (1)

T-U/* 0- + г-у)(л + 1 + г-у +

О у --1-7.---г--.

-0)2(1 + 0)2) -1-0)2

(17.90)

Неравенство (17.89) принимает вид

-(у + о)2) + /го)2(1 +?--у + п1)2)>0. (17.91)

Очевидно, что это неравенство может быть выполнено при любом о) > О, если

l+r-Y>0 (17.92)

и если h берется сколь угодно больши.м, чтобы обеспечить неравенство (17.91) при сколь угодно малых о).

Полученное условие (17.92) выполняется нри

/> у - 1, если у > 1,

?->0, еслиО<у<1,

что точно совпадает с найдепны.ми ранее условиями абсолютной устойчивости данной систе.мы (17.69) и (17.70). Смысл практической реализации этих условий был разъяснен в § 17.2.

Графически критерий устойчивости выражается в том, что вся кривая W* = и* (ы)+уТ*(а)), построенная согласно (17.90), расположена (рис. 17.19, я)

справа от прямой U* - hV* = О, обозначенной штрих-пунктиром, со сколь угодно .малым нак;юном, если 1 -1- г - у > 0. Если же 1 + г - у <0 (рис. 17.19, б), то такую прямую провести невозможно и, следовательно, нелинейная система пе будет абсолютно устойчивой.

Здесь был приведен простой пример, в котором условия устойчивости по .методу В. М. Попова выражаются в общем буквенном виде. В боль-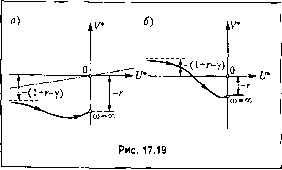