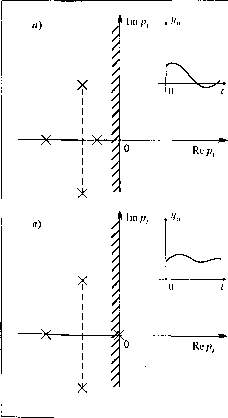Repj

/ / /

Rep,.

гле Л, и \;,- - - новые произвольные постоянные. Вызванный зтими корнями колебательный процесс затухает при а, < О и расходится при а, > 0.

Таким образом, затухание или иезатухапие переходной составляюнтей (6.9) зависит только от знаков венюствеппых корней и знаков вещественных частей комплексных корней характеристического уравнения.

Для асимптотической устойчивости системы необходимо и достаточно, чтобы вещественные части корней были отрицательньши:

Re Pi < О, г = -1, 2,и.

При это.м вещественные ко[)Пи расс\[атрива1отся как масгньи! случай комплексных корней, у которых мпи.мая часть равна пу.чю.

Нетрудно убедиться, что в этом случае наряду с (6.10) выполняются и условия (6.1) и ((5.2).

Ксли хотя бы один корень имеет положительную вещественную часть, то система неустойчива.

Представи.м корни в виде точек на колтнлекспой tlmockocih р, (рис. 6.3). Для устойчивости системы необходимо и достаточно, чтобы все корни находились па левой полуплоскости (рис. 6.3, а). Если хотя бы одни вещественный корень или хотя бы

одна пара комплексных корней окажутся па правой полуплоскости (рис. 6.3, б), то система будет неустойчивой. Таким образом, левая полуплоскость является областью устойчивости, а мнимая ось представляет собой ее границу.

В тех случаях, когда на эту границу попадает хотя бы один корень, а все остальные остаются иа левой полуплоскости, систе.ма оказывается в иекоторо.м промежуточном состоянии между устойчивостью и неустойчивостью. Для характеристики этого состояния вводится понятие границы устойчивости.

При наличии одного нулевого корняО граница устойчивости называется апериодической (рис. 6.3, в). Соответствующая этому корню составляюнщя реикния (6.9) Се* =Q, т. е. пе1)еходпая составляющая с тече1тем BpcNienn ст])емнтся не к пулю, а к Q.

В характеристическом уравнении пулевой корень [юявляется при а 0. Но чтобы это условие соответствовало апериодической границе устонитвостн, все корни уравнения

a,p ~-ap -+... + a + =0

должны находиться на левой полуплоскости.

При наличии пары чисто мни.мых корней рj., j = ±Р. (рис. 6.3, г) Г1)апица устойчивости называется колебательной. В системе в это\[ случае устанавливаются не-затухаюнию гармонические колебания с амплитудой и частотой Р,.

При наличии двух (кратных) нулевых корней р. =1 = О соответствующая и.м сумма составляющих решения (6.9), как известно, представляется в виде

(С,+С,,!:)е =C,+C ,t,

т. е. при Q+i ?t О она неограниченно увеличивается. Поэто.му в данном случае систему следует рассматривать как неустойчивую.

Все сдела1И1ые выше выводы об устойчивости относятся к линейны.м снсте.мам. Однако реальные системы практически 1Шкогла не бывают строго лшгейны.ми. Линейные дифференциальные уравнения получаются путем линеаризации (см. гл. 3), в процессе которой мшые нелинейные ч.чены отбрасываются.

Линеаризованными уравиения.ми, или уравнениями nepBoio прнближегшя стали пользоваться еще в середине XIX века, предполагая, что по ним .можно судить об устойчивости реальных систем. Строгое доказательство такой вoзroжиocти было дано Ляпуновым.

Ляпунов показал, что если в характеристическом уравнении нет нулевых и чисто мнимых корней (см, рис, 6.3, а и рис. 6.3, б), то вопрос об устойчивости или неустойчивости реальной систе.мы полностью репшется па основе этого уравпе1И1я. Однако при 1[аличии таких корней (см. рис. 6.3, в и рис. 6.3, г) поведение реальной систе.мы становится неопределенны.м, т. е. в зависимости о отброшенных при линеаризации малых нелинейных членов она может быть как устойчивой, так и неустойчивой.

При.менительио к рис. 6.3, в и рис. 6.3, г это означает, что изображе1И1ые на них процессы относятся только к строго линейным системам. Том не .менее само понятие границы устойчивости оказывается полезны.\[ и будет использоваться в дальнейшем.

Следует учитывать, что выводы Л януь[ова относятся только к описанному в ivi. 3 способу линеаризации и сиравс7УП1вы ири сделанных та.м допущениях. Для исследо-

вания устойчивости нелинейных систем общего вида Ляг[унов разработал другие методы, которые будут рассмотрены в гл. 16 и гл. 17.

Задача вычисления корней характеристического уравнения любого гюрядка при помощи средств вычислительной техники ре[1[ается достаточно просто, если параметры элеме1[Т0В системы (коэффициенты передачи, [юстоянные вре.мени) и тем самым коэффи[1иенты этого ур&впения заданы численно. На практике, однако, обычно [[бльзуются так называемыми критериями устойчивости, т. е. [[равила.ми, которые позволяют судить об устойчивости без вычисления корней. Ценность этих критериев состоит не только и даже не столько в том, что устраняется ь[еобходимость вычисления корней. Они дают воз.можность установ[1Ть, как тот или иной нара.метр и структура системы в цело.м влияют на устойчивость и как их следует изменить, чтобы система стала устойчивой.

Наиболее простым, хотя и ограииченпы.м но своим воз.можностям критерием является необходимое условие устойчивости.

Необходимым (но пе достаточным) условием устойчивости системы является положителгтостъ коэффициентов ее характеристического уравнения.

Это значит, что при [юложительпости всех коэффи[1иентов системлможет быть устойчивой, но [[е исключается возможность ее [[еустойчивости. Око[1чате;[ьный вывод .можно сделать применив, напри.мер, критерий Гурвица (см. § 6.2). Если же не все коэффицие[[ТЫ положительны, то система наверняка не может быть устойчивой и никаких дополнительных исследований не требуется.

Необходимость положительности всех коэффициентов характеристического уравнения системы любого порядка устанавливает критерий Гурвица. Для систе.м первого и второго порядков необходи.мое условие является и достаточпы.м, в чем нетрудно убедиться прямы.м нахождением корней уравнения,

Исследование устойчивости любой системы всегда полезно начинать с проверки выполнения необ.ходимого условия. В качестве иллюстрации рассмотрим три примера.

Система второго порядка, характеристическое урав[1ение которой

Tp+kT2P+k-]:0,

всегда устойчива при > 1.

Система третьего порядка, характеристическое уравнение которой

Ti%P + T{p+ikT2-T;i)p + k-\0,

может быть устойчивой, если k> 1, kl\ > Г3.

Система, характерист[1ческое ypaB[[einie которой

Tj2pUT, + T2)p + p + k = 0,

структурно неустойчива, так как коэффицие1[т 3 = О и не может стать [[оложитель-ным ни при каких значениях пара.метров. Для обеспечения устойчивости такой систе.мы необходимо изменит1> ее структуру, например, за счет введения корректирующих звеньев (см, гл. 10), что приведет к изменению характеристического уравнения.