§ 11.7. Прохождение случайного сигнала через линейную систему

Рассмотрим .тииейную систему (рис. 11.25) с передаточной функцией W (р) и функцией веса w(t). Пусть па входе действует случайный сигнал (() с корреляционной функцией К](г, ?]).

Выходной сигнал Х2 (t) на основании фор.мулы свертки (7.44)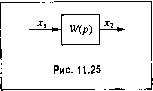

Х2 (О = (т)-! (t - т)й?т = jia(t - т)х, (т)(7т.

Рассматривая в этой формуле .математические ожидания, имеем

MX2(0J = xt) = \w(t-x)x, (T)dz.

(11.95)

Для получения корреляциопной функции па выходе запипюм исходную форму-1ля центрирован! моментов времени;

лу для центрированных значений x(t) = x(t)-x(t) и Х2(0 =-2() ~-2(0 для двух

4(0= Jда(тlK(-лVr-o

x2(t)=lw(X)x(t,-X)dX. о

(11.96)

После перемножения получим

4(04(fi)- JJ?(Ti) w(X)x?(t, -Т1)х?((,-X)dy]dX.

(11.97)

Далее, переходя к математическому ожиданию, можно найти корреляционную функцию

4(i,t)= jw(r])dr]jr&(X)R(t-r],l-X)dX.

(11.98)

Для определения дисперсии па выходе D2 (t) в формуле (11.98) следует положить г Тогда

D2(t) = R{Ct)= jw{ц)dцjz0(X)RUh - Л,г,-X)dX. о о

В случае использования кано1гического разложе1гия случаЙ1гой функции

j:,(f) = i,(0 + ZK--v(0 (11.100)

выходная величина может быть представлена в виде

.r2(0 = i2(0 + ZK-i/v(0. (11.101)

где x2{t) определяется формулой (11.95), а координатные функции

y (t)= jw(t-x)xy(x)dT. (11.102)

Корреляционная функция выходного сигнала

R2it,ti) = Y,F>vyA0yv(ti) (11.103)

а дисперсия

£2(0 = Z£v[.Vv(0f. (11.104)

Для нахождения математического ожидания X2(t) и координатных функций yit) в соответствии с выражения.ми (11.95) и (11.102) могут иснолызоваться различные методы построения переходных процессов (см. главу 7).

В случае, когда на входе (рис. 11.25) действует случайный стационарный процесс, корреляционная функция /?, (?, t,) = /?f(x) зависит только от сдвига х = - I.

Однако на выходе линейной системы процесс некоторое вре.мя после включения будет устанавливаться и не будет стационарным. Корреляционная функция на выходе может быть получена из o6niero выражения (11.98):

R2(t,t) = lw{ц)dцjw(X)R(x-ц + X)dX, (11.105)

а дисперсия - из (11.99):

D2(t)=jw(r])dr]jw(X)R(X-r])dX. (11.106)

0 0.

Если рассматриваемая система устойчива, то Rl{t,t) и (О стремятся к некоторым пределам, которые определяют стационарный процесс на выходе. Они могут быть найдены из (11.105) и (11.106), если положить го° и °о.

332 Непрерывные линейные системы автоматического управления Тогда при 1.1- t = T

(11.107)

D2 = R(0)= да(п)й?г1а,(л)7?, (-пУл

(11.108)

Пусть, например, иа входе иптсгрируюн1его звена с передаточной функцией W(p) = k/p и функцией веса ш (t) = k действует бел1лй шум с корреляционной функцией 7?, (т) = 7?f (т) = yV5(t). Тогда в соответствии с (11.106) дисперсия па выходе будет

7)2 (О = \kdy] = \kN5(X -r])dX= \kdц kN = kNt,

0-0 0

т. е. дисперсия растет пропорционально времетт Нетрудно видеть, что D (оо) -> оо, так как звено пе является устойчивым, а оно тшходится на границе устойчивости (нейтрально-устойчиво).

Для расчета установивптегося стационарного процесса па выходе системы (рис. 11.25) более удобно исходить из известной спектральной плотности па входе 5) (со). Тогда можно легко найти спектральную плотность 52 (со) выходного сигнала. Действительно, по определению снектра.мьная плотность иа входе связана с изображением Фурье 71 (/ш) случайной величины х, (t) соотношением (11.61):

5, (со) = lim - 7 , (7(0)

/->-2Г

Это же соотношение имеет место и для выходного сипшш:

2(to) = ,.iniT2(7to)f

/ - >~ 21

В линейной системе изображения Фурье t\ (/ш) и 2 Ом) связаны между собой посредством частотной передаточной с{)ункшп1:

7-2 (/со) - W(jti))F(J)-

Отсюда .можно найти

52(cй) = liml(ia)) W(j(xi)

52(со)=1(;со)5,(со).

(11.109)

Таким образом, спектральная плотность выходной величины может быть no.iy-чена умножением спектральной плотности входной величины на квадрат модуля ча-