Линии Wj,(C,+j(>i) у при const

не зависят от частоты ю и показателя затухания , что и.меет место для нелинейностей видаУ-Хх). В .этом случае после подстановки в характеристическое уравнение р = С, +jw выражение (20.18) .можно представить в виде

W (fl)

(20.38)

где обозначено:

W ( ) = ( ) + M ); W,( + ; ) = gi, (20.39)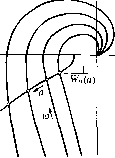

о а

Рис. 20.4

причем числитель и знаменатель последнего выражения п редстав л я ют собо й, со гл ас п о (2 0.19), .м но гоч л ен ы п о сте-неням jo с коэффициентами, зависящими от С

Задаваясь различными постоянными значениями , нострои.м серию кривых W. ( -гjo) как функции orjo при = const (рис. 20.4) аналогично то.му, как обычно строятся амплитудно-фазовые характеристики линейной час-

ти системы. На том же графике (рис. 20.4) нанесем липию

. Точки пересече-

ния ее с линиями ( + j(a) определяют собой рещепие уравнения (20.38), а именно для каждого значения х в .этих точках пересечения получаются соответствующие значения а (по кривой ТТГуТ ) и ( кривой И-, ( + jo.))). Этим са.мы.м определяется

качество колебательного переходного процесса при всех заданных параметрах систе.мы, т. е. определяются точки одной вертикали на диаграм.ме качества (рис. 20.2). Повторив такие же построения (рис. 20.4) для ра.зличных .значений выбираемого пара.метра системы k, .можно построить и всю диаграм.му качества (рис. 20.2).

Способы построения диагра.мм качества для систем второго класса и другие ири.менеиия диаграм.м см. в [72]. Там же рассматриваются несимметричные колебательные процессы и скользящие процессы.

§ 20.2. Примеры исследования колебательных переходных процессов

Рассмотрим С1Гачала построение диаграммы качества и кривой переходного процесса на примере нелинейной следящей системы, азатем исследуем переходный процесс в пелипейпой системе с логическим устройство.м.

Пример 1 . Структурная схема следящей системы изображена па рис. 20..5, где 1 - датчик рассогласования, 2 - усилитель, 3 - реле, 4 - исполнительный двигатель, 5 - редуктор, 6 - управляемый объект, 7 - дополнительная обратная связь.

Рис. 20.5

Рис. 20.6

Систе.мы с такой структурной схемой находят нри.менение в тех случаях, когда для управления двигателем нужна значительная мопиюсть, а увеличение габаритов и мас-сы усилителя нежелательно.

Для датчика рассогласования системы имеем уравнения

u=ky{a--[) = kfi, (20.40)

где а и Р - соответственно входная и выходная величины системы; к, - коэффициент передачи датчика рассогласования; Ь - рассогласование.

Статическая характеристика нелинейного звена - реле - изображена на рис. 20,6. Выполняя гар.моническую линеаризацию пелипейпой характеристики реле, получим уравнение

з = ?( ) 2. (20.41)

где в соответствии с (18.16) для однозначной релейной характеристики с зоной нечувствительности коэффициент гармонической линеаризации определяется формулой

(20.42)

Учитывая уравпение датчика (20.40), гармонически линеаризованное уравпение реле (20.41) и передаточные функции других линейных звеньев, приведенные нарис. 20.5,запицюмуравнепиедля собствинюгодвижения (а = 0) следящей системы в виде

[(Г, р + 1)(Г2р + 1 )р + kkAq (а)р + kAhKq ( )] Щ = 0. (20.43)

Характеристическое уравнепие, соответствующее полученному, диффереппиаль-ному уравнению, будет

(Г,р +\){1\р +\)р + k2k2kq (а)р + kAhkiq (а) = О- {2Q.AA)

Произведем вначале построение диаграммы качества по нерво.му способу, указанному в § 20.1. Для этого в уравнении (20.44) необходимо произвести подстановку р = С + ioD с использованием формулы (20.19).

Вычисляя соответствующие производные характеристического полинома (20.44) пор и подставляяр = в полученные выражения производных, найдем коэффициенты

[)а:);10жения в ряд уравнения (20.44) при рС,+ joi, которое в ре;)ул1лате распадается иа следукмцие два уравпепия:

X = Г, ГзС + (Г, + Т,)С + [1 + МзМ( )]С + к,кфф,д{а) -

- [ЗГ,7,С + 7, + Г,]а)2 = 0; (О-

У = IЗГ, Т + 2 (г, + + 1 + к2кф ,с](,а)]1И - 7, Tin = 0. ( 20.46) Из последнего уравне1Н1Я определяем квадрат частоты:

о = -Vi;,?-, + 2 (71 + )с +1 + 2зо<:/( )]. (20 47)

Подставляя значение со в уравнение (20.45), получим

Т,72 + (7, + 7,) С + [1 + Woc9( )l С + k.kk.qia) =

pir 37ГгС- + 2(7, + Го) i;+ 1 + М.зМ( )] WJ,: Т, + Т,].

(20.48)

Построи.м диаграм.му качества для следящей систе.мы по параметру ку Так как затухание в (20.48) входит нелинейно, то удобно данное уравнение разрешить относительно параметра В результате получим

, , , , , ITJ/ + 2 (7, + 7-2) С +1 + k2k,k ,q(a)]x к2к,кМа)\ТгГ2

х(щи+/i + h) - [ТМ + + 72) С + С]}.

Для построения диагра.ммы заугадимся следующи.ми значениями других 1шрамет-ров: Г, = 0,05 с, 72 = 0,05 с, /2 = 1, = 200 град/с в,к = 0,01, к = 10 с В/град, 6 = 5 В, с =120 В.

Подставляя приведенные значения параметров в (20.49) и задаваясь различными постоянными значениями шжазателя затухания С, = con.st, строим кривые а (к) (рис. 20.7). 11а основании формулы (20.47) при постоянных ;шачениях частоты со = const строим также пунктирные кривые а (k). Эти кривые иредставляют собой диаграмму качества для рассматриваемой следящей системы. Кривая а{к) при i; = О соответствует автоколебашшм.

Выполни.м теперь построение диаграм.мы качества по второ.му способу, указанному в §20.1.

Уравнение (20.44) ;!апнше.м в виде

/; +Л,;?--Л2/?+Л.; = 0,

hh \2