-90°

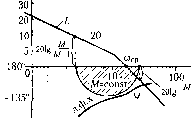со, с

Рис. 8.24

Из выражения (8.86) можно найти, в частности, максима.1ьный запас но фазе обычным методом отыскания максимума:

1 Vm

M-max - arccos-рг = arccos-

(8.88)

Этот максимум получается, когда модуль A = yjc . Если имеется построепная л. а. x. (рис. 8.24), то по имеющимся р.-кри-вы.м и при заданно.м значении М можно достроить требуемое значение загаса по фазе для каждого значения модуля. Это постро-enire должно делаться для модулей, лежа-И1ИХ в пределах (8.87). В результате будет получена запретная область для фазовой характерисгики. Чтобы показатель колебательности был не больше заданного значения, фазовая характеристика не должна заход1гть в эту область. Нетрудно видеть, что определение качественного показателя, характеризующего запас устойчивости, делается здесь одновременно с 01гределепием устойчивости.

Удобство показателя колебательности определяется также тем, что запас устойчивости характеризуется здесь одним числом, имеюиим для достаточгго широкого класса систем сравнительно узкие пределы (1,1 + 1,5).

Если в полипоме числителя передаточной фуикпии разо.мкнутой системы W{p) нет корней с гюложительной вещественной частью, то возможность получения требуемого запаса устойчивости за.мкнутой систе.мы может быть предварительно установлена непосредственно по виду л. а. х. разомкнутой системы. Такая возможность существует, если л. а. х. в окрестностях частоты среза C0j., (рис. 8.25, а) или вблизи нее (рис. 8.24) имеет асимптоту с иаютоном -20 дБ/дек (или с нулевым наклоном, что встречается гораздо реже). На рис. 8.25, а протяженность этой асимптоты h = Шг/ш,. Чем больше h, те.м больпге ожидаемый запас устойчивости. Чтобы убедиться в этом, рассмотрим два предельных случая.

Пусть л. а. x. состоит только из одной асимптоты с наклоном -20 дБ/дек (рис. 8.25, б), что соответствует передаточной фупкпии W {р) = К/р. Тогда замкну-

-180

-90°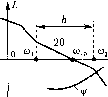

W -180°

-90°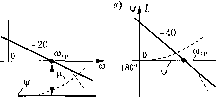

тая система очень хорошо демпфирована, так как запас устойчивости по амплитуде 1 = оо, но фазе р.; = 90 , а показатель колебательности (см. рис. 8.2.3) М = 1, При наличии дoпoлнитeплloгo излома (показано пунктиром на рис. 8.25, б, а также см. рис. 8.24) запас устойчивости уменьшается.

Пусть теперь л. а. х. состоит из одной асимптоты с наклоном -40 дБ/дек (рис. 8.25, в), что соответствует передаточной функции W{p) = К/р. Нетрудно убедиться, что в этом случае замкнутая систе.ма находится на колебательной границе устойчивости, а при наличии дополнительного и.злома (показано пунктиро.м) становится неустойчивой.

Таким образом, если л. а. х. разомкнутой chctcyhjI пе и.меет асимптоты с наклоном - 20 дБ/дек (или с иулевы.м наклоном), то ие обеспечивается даже устойчивость замкнутой системы.

Bo;iee дета;м>110 связь .между запасом устойчивости и протяженностью h будет рассмотрена в §12.6.

Оценка быстродействия может производиться по частотгимм характеристика.м замкнутой и разомкнутой системы. При рассмотрении замкнутой системы обычно исноль.зуется амплитудная частотная характеристика (рис. 8.19).

Для оценки быстродействия по этой характеристике могут использоваться сле-дуюн1ие величины:

со - резонансная частота, соответствующая пику а. ч. х.;

со - частота, соответствуюишя полосе пропускания за.мкнутой системы и определяемая из условия А (со ) = 0,707;

(И - частота среза, соответствующая условию А (со ) = 1;

сОз - эквивалентная полоса пропускания замкнутой системы, определяемая по выражению

Ыз = 11 Ф( й?a), (8.89)

где I Ф (/со) I = А (со).

Эквивалентная полоса пропускания представляет собой основание прямоугольника (рис. 8.19), высота которого равна единице, а площадь равна площади под кривой квадратов модуля Ф (/со).

В отличие от показателя колебательности, который является ггекоторой безразмерной характеристикой и лежит в сравнительно узких пределах, приведеггные вгягпе характерпгяе частоты, онределягоиие быстродействие системг>г, и.меют размерггость и их допустимые значения .могут сильно меняться в зависимости от типа и назначения системы. Здесь наблюдается полная апа-тогия с критериями качества, осггован-ггыми на рассмотрении кривых переходггого процесса. Допустимое зпачеггие ггерере-гулирования а % (рис. 8.3) лежит в сравнителыго узких пределах для систем самого различного назначения, а допустимое время переходггого ггроцесса t может меняться от долей секуидг)! до нескольких часов и более.

Допустимгяе значения сОр, со , м или со до.тжиы устанавливаться для гсаждой конкретной системы на основе изучения условий ее эксгг.туататгии. При :отом харак-

Ф(р) =

1 + 2СГр + Г

(8.90)

Для этой передаточной функции сравнительно просто найти, как зависят величины, которые определяют запас устойчивости: перерегулирование а%, показатель колебательности М и запас устойчивости по фазе р от пара.метра затухания . Соответствующие кривые приведены на рис. 8.26, а. На

а) а% Из

50 100

40 80

30 60

20 40

10 20

О 0,25 0,50 0,75 ?

2,0 М

рис. 8.26, б дается зависимость между перерегулированием а% и показателем колебательности Ы для той же передаточной функгши (8.90).

Кривые, приведенные на рис. 8.26, в некоторой мере характеризуют связь между показателями качества и в более сложных случаях, чем выражение (8.90).

теризовать быстродействие системы может как вся совокупность указанных выше величин, так и каждая из них в отдельности.

При определении быстродействия но частотной передаточной функции W (ju)) разомкнутой системы может использоваться частота среза ыр, которая определяется из условия mod W(/cop) = 1 или L ((лр) 0. Эта частота показана, например, на рис. 8.2 и 8.24.

Определите частоты среза ра;юмкпутой системы может быть сделано па диаг-ра.мме, изображенной па рис. 8.18, по точке пересечения а. ф. х. с окружностью единичного радиуса, центр которой расположен в начале координат.

Резонансная частота замкнутой системы Ыр близка к частоте колебаний системы в переходном процессе. Значение сОр может быть приближенно определено по точке а. ф. X. (рис. 8.18), которая ближе всего расположена к точке (-1,;0).

Частота среза (ор во .многих случаях близка к резонансной частоте системы (Ор.

Удобной и наглядной .мерой быстродействия системы является также частота со (рис. 8.2), при которой задающее воздействие вида g = g. sin ш,/ отрабатывается системой с амплитудой ошибки пе более х ,,..

Хотя приведенные выше частоппле критерии запаса устойчивости и быстродействия могут рассматриваться независимо от свойств системы во временной области, представляется полез1№1М провести некоторое приближенное сопоставление частотных и вре.мегтых характеристик.

Если показатель колебательности М > 1, то замкнутую систему можно аппроксимировать ко.чебательным звеном (см. § 4.5). Тогда передаточная функция замк1[у-той системы .может быть представлена в виде