Продифференцировав (6.51), иолучае.м

откуда

р!1 р.

fc-i

(6.52)

где а - скорость звука в газе, определяемая формулой

Обычно не учитывают сопротивления движения газа в трубопроводе, пренебре-

Ъге Эр

гая сравнительно малыми членами да-- и w-. Кроме того, ввиду малости величи-

Э/ Э/

пы отклонения давления р в процессе управлетгия от его установившегося значения

можно считать, что -7г = 1, а следовательно, согласно (6.51) -7г~1. в результате из р р

уравнений (6.49), (6.50) и (6.52) получаем

bw \ Ър дш< 1 Эр

dt р Э/ Э/ pOfl2 dt

(6.54)

Ведем обозначения для относительного отклонения ф управляемой величины от ее установившегося значения и для относительной координаты л вдоль трубопровода:

р-р Др , /

= 7 (6.55)

р р л

а также для относительного отклонения у скорости движения газа в трубопроводе:

V = -rr-k-, (б.об)

где - скорость газа в трубопроводе при установившемся процессе; к - показатель степени в адиабатическом уравнении состояния газа (6.51).

Переходя в уравнениях (6.54) к этим относительны.м безразмерпы.м переменным и бесконечно ма.1ым приращениям, получаем искомые уравнения управляемого объекта (трубопровода) в виде

у27;д = *Р. т = - (6.57)

Э ЭХ dt dX

где введены два постоянных параметра управляемого объекта:

(6.58)

Первый из них (Гц) представляет собой, очевидно, время прохождения газа ио дапно.му трубопроводу в установившемся процессе, а второй (у) - отно1пение установившейся скорости 1-аза к скорости звука в нем.

За.метим, что уравнения (6.57) эквивалентны так называемому волновому уравнению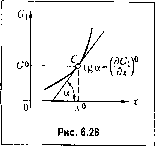

Y 0 2

ЭГ Эл

(6.59)

которое легко [юлучается, если первое из уравнений (6.57) продифференцировать но X, а второе - по Сч сравнить результаты диффере1Н1ирования.

Для системы уравнений в частных производных (6.57) надо написать граничные условия. Для этого запишем уравнение поступления газа через клапан в начале трубопровода и уравпепис потребления газа в конце его.

Исполызуем выражение для скорости газа через его расход, а именно:

(6.60)

где G - расход rarsa по весу в секунду; F- плон1адь сечения трубопровода; g - ускорение силы тяжести.

Условимся значения всех переменных, относящихся к началу и к концу трубопровода, обозначать индексами 1 и 2 соответствеппо. Расход га.за в начале трубопровода С будем считать функцией координаты неремеП1епия клапанах, т. е.

G, = G,(x). (6.61)

Эта функция (рис. 6.28) определяется либо аналитически.м расчето.м, либо из опытных да1шых.

На основании уравпепий (6.60), (6.61), а также формул главы 3 малое отк.то1ге-ше Д?£), величины скорости в начале трубопровода от се установившегося значения (!° будет

щ - = Aw, =

APi =

AG -

-Ар, =

Ax -

(6.62)

(установившиеся значения да , (у, р пишутся без индекса 1, так как они одинаковы

ЭС,

вдоль всего трубопровода). Величина

есть тангенс угла ггаклона касатель-

ной в точке С (рис. 6.28), соответствующей установившемуся процессу в трубопроводе. На основании (6.51) и (6.5.3)

,2

Введем безразмерную величину относительного отклонения управляющего клапана:

х-х Ах

(6.63)

гдех - условное номинальное значение, равное

\0

(6.64)

Кроме того, заметим, что согласно (6.60)

(6.65)

Подставляя все это в (6.62), с учетом (6.56) и (6.55) получаем уравнение поступления газа через управляющий клапан в начале трубопровода:

(6.66)

которое является первым граничным условием для уравнений объекта.

Расход га,эа в конце трубопровода у потребителей можно записать согласно (6.60) в виде

G2=FgP2U2.

(6.67)

С другой стороны, известно, что при выходе газа из трубопровода (в случае критического истече1гия, которым мы для простоты и ограничимся) будет

(6.68)

где Q - площадь некоторого эквивалеппюго выходного сечения на конце трубопровода у потребителей (.это величина, которая может меняться как угодно по ироизво-