где xj,х - неременные, описывающие поведение исс.тедуемой системы.

В э.чектронной моде.ти должна быть реализоватга совокупность ди<})ференциаль-пых уравнений аиатогичггого вида:

1Щ clXj

?/2, г/т

(7.46)

где Х - машинные иеремепные (обычно напряжения), соответствующие ис-

следуемым переменным х х ; от,- = Х,/х; - масштабные ко:-к})фнпие11ты, связыва-юнще исследуемые перемешгые с соответствующими им машинными неременнылн!, т, = i/t -- .мас1птаб времени, связываюпин! пстинное время протекания процессов t с времене.м протекания процессов в модели т.

За.метим, что из.мененпе скорости протекания процессов во;)мож1ГО го.тько п[)и полном моделировании всей системы. При моделировании только части системы и сопряжении ее с реальной аппаратурой необходимо вынолпение равенства т = /., т. е.

?77, = 1.

При выборе .масштаба времени должно учитываться то обстоятельство, что элек-т])онпые модели могут точно работать при ограпичшпюм времени протекания моделируемого П[юцесса. Это время не должрго обычно превышать нескольких сотен секунд, что связано с особетюстя.ми работы :)лектрониых интеграторов.

Масштабные коэффициенты ОТ; должны выбираться таким образом, чтобы в переходных процессах макси.ма-чьное значение магпинной перемеииой] X,- \ = т,.Х: , .,J не превосходило предельного допустимого значения.

Суп1,ествуетлве раз1ювидпости эле1арощ1ЫХ кюделируюнптх манит: моде;п1 струк-туртюго типа и .модели .матричного типа. Первые позволяют моделировать структурную схему систе.мы, что во многих случаях оказывается более удобт>1.м и наглядпы.м.

Модели матричного типа требуют записи дифференциальных уравнешп! исследуемой систе.мы в особой, матричной форме. Матричные модели менее удобны для исследования систе.м и потому исноль.зуются реже.

Остановимся вначале па п.меющих наибольшее применение моделях структурного тина. Они построены на базе так на;шваемых операциоппых усилтхлей, \ш-полняющпх операции интегрировапня, суммирования и умноже1ГИя иа постоя1ИН)1Й .мтюжитель.

Операгпто1И1ЫЙ усилитель представляет ct)6on усил итель ностояшюго тока с боль-1НИМ ко.эффицие1ггом усиления по нап[5яжснию (десятки н сотни тысяч). Динамические свойства усилителя таковы, что он может быть замкнут 10()%-ной отрнпа-тельной обратной связью через резистор или конденсатор без потери уст011ЧИВосги (без генерации) в замкнутом состоянии.

Передаточная с}ункция усилителя, замкнутого обратной связью (рис. 7.3) Н[)и большом коэффициенте усиления может быть достаточно точно представлена в виде

,.ых(Р) го(р) .

им hip)

где 2i(p) - входное сопротивление усилителя в операторной форме, Zq{p) - сопротивление в цепи обратной связи.

1 JJal

1 Г-- 1

>

1.1 мм-fe

Рис. 7.3

в) R

1 XLLl

-ih

Рис. 7.4

Знак минус в формуле (7.47) показывает, что операцнопный усилитель инвертирует входной сигнал (.меняет его знак). Современные усилители обгячно и.меют как ипвертируюпп1Й, так и иеинвертирующий входы.

Рассмотри.м три основных режи.ма работы усилителя.

1. При Zq(p) = /?о и г,(р) = /?, усилитель выполняет функцию умножения входной величины на постояппг>1Й множитель (рис. 7.4, а):

(7.48)

Упрощенное изображение такого усилителя нсжазапо па рис. 7.4, а справа.

2. При Zq(p) = 1 /рС, что соответствует установке в цепи обратной связи конденсатора, и 2, (р) = /? усилитель работает в режиме интегрирования входной величины (рис. 7.4, бу.

и..Лр) = -им = --иМ-

кСр р

(7.49)

Два варианта упрощенного изображения такого усил1гтеля изображегил на рис. 7.4, б справа.

3. При 2о=7? и 2(р) =1/рС, что соответствует установке конденсатора во входной цени, усилитель работает в режи.ме дифференцирования (рис. 7.4, в):

- -RCpUM = -k.pUM- (7.50)

Упроп1енное изображение такого усилителя показано па рис. 7.4, в справа. Режим дифференцирования обычно не используют при моделировании, так как в этом режиме сильно возрастает- влияние высокочастотных по.мех и паводок.

На рис. 7.,5 изображен операционный усилитель в режи.ме сум.мирования. Как нетрудно показать, при Zq(j)) = R(,

fBb,x(P) = --Z-Б-

(7.51)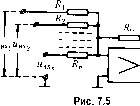

При 2о(р) = 1/рС, получаем суммирующий интегрирующий усилитель.

В табл. 7.3 приведены типичные случаи использования операционного усилителя для получения различных динамических звеньев.

В таблице использован машинный оператор дифференцирования

dl dt nil

(7.52)

При моделировании в натуральном масштабе вре.мени т = г и Р = р.

Электронная модель структурного типа имеет в свое.м составе несколько операционных усилителей, которые могут работать в режиме интегрирования, т. е. с конденсатором в цепи обратной связи. Число этих усилителей опреде.тяет наивысший

Таблица 7.3. Типовые динамические звенья электронных моделей

Схема

HH=i-1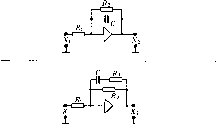

Передаточная функция

W(P) = -~, T=RC

W(P) = -

\ + TP

k = , T = R2C

W{P) = -k

1+Г1Р

k = -, T,=R.,C, 72=( 2+ 3)C

W{P) = -

Ti=R,C, Г2= 2С