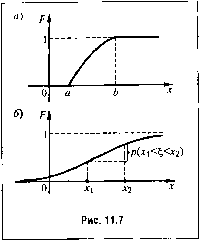Г010, ЧТО непрерывная случайная величина примет онределеппое числовое значение х, бесконечно мача (нанри.мер, вероятность пolIaaпия центра тяжести снаряда в оиределенную точку це;ш). Вероятность же того, что непрерывная случайная величина окажется в некотором промежутке Х <х< х-, будет иметь конечное значение, а именно:

P(X,<<X2) = F(X2)-f(x,).

Вероятность того, что пенре])ывная случайная величина содержится в промежутке между х и

X + dx, буд(т

Р{х <%<x + dx) = dF(x) = dx.

Величина dFix).

- = w(x)

(11.11)

называется плотностью вероятности.

Закон распределения для непрерывной случайной величины в отличие от дискретной задается не в виде значений вероятности, а в виде плотности вероятности х0 (х), называемой также дифференциальным законом распределения. На рис. 11.8 показаны диффepeнпиaJПДIыe законы раснределепия для двух вариантов функции распределения F{x), показанных па рис. 11.7. Если бы здесь использовалось го же понятие закона расн1)еделення, что и для дискретной случайной величины, то получились бы бесконечно .малые ординаты Р {х).

Выражение w (х) dx означает вероятность того, что случайная величина содержится .между X и X + dx:

Р (х < < X -I- dx) = w (х) dx.

Вероятность того, что случайная величина содержится между зиачения.ми х, и Х2, определяется фор.мулой

Р(х, < < Х2) = j да(х) <х,

(11.12)

что геометрически выражается заштрихованной площадью иа рис. 11.8. Кроме того, имеет место зависимость

F{x)= jw(x)dx . (11.13)

Вся площадь под кривой w (х) равна единице:

jw(x)dx = l, (11.14)

так как F(°°) = 1.

Формула (11.14) соответствует .мо.менту нулевого порядка. Среднее значение (математическое ожидание) соответствует мо.менту первого порядка:

xw{x)dx

(11.15)

что вытекает из формулы (11.5) как предел суммы.

Моменты высших порядков но аналогии с (11.6) будут

+<

х = \х т{х)с1х.

(11.16)

Таким же образом можно вычислить центральный мо.мент /и-го порядка

M\{x-ir\=\{x-i) z0{x)clx. (11.17)

Как и в случае дискретных случайных величин, центральный .момент первого порядка всегда равен нулю.

Рассеяние непрерывной случайной величины можно оценивать одним из следующих значений, словесные формулировки которых остаются прежними.

Среднее отклонение (мало удобная для вычислений величина)

Д= \x-x\w{x)dx.

Дисперсия (наиболее удобная для вычислений величина)

+~

D= {x-xfw{x)dx = x-{xf.

(11.18)

а) ге

Рис. 11.9

Срелнеквалратичпое отклонение

a = fD=7-{xf. (11.20)

Средневероятны.м отклонением Д на,зывает-ся такая величина, при которой отклонения \х-х\<А и \ х-х\>А имеют одинаковую вероятность.

Рассмотри.м простейнше типовые законы распределения непрерывных случайных величин.

1. Равномерное распределение случайной величины на определенном участке характеризуется плотностью вероятности w (х) и функцией распре деления f (х), показанными иа рис. 11.9.

При этом на основании свойства (11,14) и.меем

с = -

Подсчитаем характерные значения. Среднее значение (математическое ожидание)

х=хда(х)Лг= xcdx =

b + a

Среднее значение квадрата случайной величины (.момент второго порядка)

х2 =

2 J a-+ab + b X сох =-.

Дисперсия

0 = х-(хУ = Среднеквадратичное отклонение

,2 ,ч2 (Й- Г

Средневероятное отклонение

Д., =-(b-a)<G. 4

Максимально возможное отклонение случайной величины от среднего значения в данном случае будет