При этом из (19,62) находим;

а, = а =

1

r;v,+i

2 s2

(19.64)

(19.65)

причем изменяются, конечно, и формулы для ж , и со (их можно получить таким же способом). Подбором параметров системы амплитуду автоколебаний опшбки й, .можно сделать весь.ма малой.

§ 19.2. Прохождение медленно меняющихся сигналов в автоколебательных системах

Рассмотри.м очень важный для практики случай, Koriia внеипгее во;действие/(t), которое может быть либо возмуииющим, либо управляющим (задаюпшм), в автоколебательной системе является не постоянным, а медленно .меняюпщмся. Медленно меняюнюйся будем называть такую функцию времени, которая сравнительно мало изменяется за пе1)Иод автоколебаний, т. е, соблюдается условие в виде одного из неравенств

/(+Г)-/(о /(0

T f(t.)

где Т = -, а со - частота автоколебаний, со

Соответственно для астатических систем медленно меняющейся скоростью / (О будет такая, для которой выполняется устовие

/\t+T)-f(t) fXt)

T f{t)

Указанными свойствами почти всегда обладают полезные сигналы управления, проходящие через автоматическую автоколебательную систему (в том числе в переходных процессах).

Условие медленного измепет1Я любой функции вре.мени можно выразить также и в частотной форме, а имен1ю: .медленно меняющейся считается такая функция, возможные частоты изменения которой во времени значительно ниже возможной частоты возникаюп1его в системе периодического решения (авгоко.юбаиий).

Сделанные предположения позволят величину / {I) или, ссютветствепио, pf {t) считать постоянной :sa вре.мя каждого периода исследуемых автоколебаний и искать решение в той же форме (19.4):

л- = д- -н.г*, x* = asm(uf.

Q(p)(x4x*)-bft(p)

F+qx*+px*\ = S{p)f{t). со j

При достаточно медленном изменении функции/(t) (а в астатических сисггемах pf) и величии х , а, со, входящих в коэ(})фициенты i, q, q, данное уравнение .может быть ра.зд€лено на два отдельных уравнения:

Q(p)x4ft(p)f=5(p)/(0, (19.66)

Q{p)x*+R{piq + p\x*Q, (19.67)

соответственно для .медленно .меняюи1ейся составляющей и для колебательной состав-ляюн1ей. При это.м ра.зделепии уравпештй, как и прежде, сохраняются существенно нелинейные свойства систе.мы.

Следовательно, здесь сохраняется целиком прежний (§ 19.1) первый метод решения задачи (второй здесь неприемлем), выраженный формула.ми (19.10) - (19.1,3), где в данном случае х** является величиной не постоянной, а медленно меняющейся. Поэтому прежний процесс решения заканчивается определением функции смещения (19.13). Подставив (19.13) в (19.66), получим дифференциальное уравнение для онре-делепия .медленно меняющегося сигнала управления х {t) (на с})оне автоколебаний системы) в виде

Q(p)x4/?(p)O(x )-,9(p)/(0. (19-68)

Таким образом, получается, что для определения медленно меняющихся процессов функцию смещения

P-Oix) (19.69)

следует подставить в уравнение автоматической системы (19,1) вместо заданной нелинейности f(x,px).

Следовательно, функция смещения Ф (х ) представляет собой как бы статическую характеристику (обычно криволинейную), которая определяет зависимость .между выходной и входной величина.ми .задашюй нелинейности для ностоянных или медленно меняюн1ихся сигналов в автоколебательной системе.

При любых пелипейпостях, в том числе и скачкообразных, (})упкция смешения Ф (х ) может получать при онределепных условиях вид весьма плавной кривой. Этот

где t отсчитывается отдельно внутри каждого периода, ибо теперь х , й и со будут ие постоянными, а переменными во времени Г (от периода к периоду) вместе с изменением внешнего воздействия/{t). При этомх (/:) будет медленно меняюпщмся сигналом на входе нелинейнос;ти.

В связи со сказанным здесь остается в силе разложение (19.5) - (19.7). Но подстановка его в заданное уравнение нелинейной автоматической системы (19.1) дает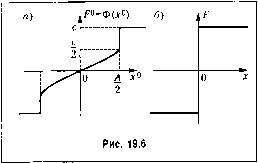

эффект называется вибрационным сглаживанием нелинейностей при помощи автоколебаний, а функцию смещения Ф (.г ) можно называть сглаженной нелинейной характеристикой.

Так, в при.мере § 19.1 согласно (19.40) функция смещения будет иметь вид рнс. 19.6, а, т. е. для .медленно .меняющегося сигнала в даппой релейной системе нелинейная характеристика будет в определенных пределах иметь плавный вид (рис. 19.6, а) вместо скачкообразного (рис. 19.6, б) - за счет сглаживающего влияния автоколебательных вибраций.

Далее, например, для нелинейностей, обусловленных зоной нечувствительпости (рис. 19.7, а), а также зазоро.м (рис. 19.7, б) и петлей, сигналы х < h при отсутствии автоколебаний ие передаются (F= 0). При наличии же автоколебаний сигиа.! < h передается в виде составляюп1ей Поэтому для медленно меняюн1егося сигнала получается плавная характеристика (функция смещения) Ф (х ) без зоны нечувствительности (рис. 19.7, б). Эффект вибрациощюго сглаживания нелинейностей в этих примерах является положительны.м (ликвидация зон нечувствительпости и петель).

Однако в других случаях эффект вибрационного сглаживания нелинейности может оказаться и отрицательным. Возьме.м, например, нелинейную характеристику с зоной насыщения (ограниченно-линейную), показанную на рис. 19.8. В этом случае за счет того, что верхущки сшгзсонды с одной стороны срезаются, постоянная составляющая 7 будет меньще, чем са.мо значение f, соответствующее линейному начальному участку. Поэтому постоянный или .медленно меняющийся сигнал будет при наличии автоколебаний проходить через да1П1ую нелинейность с меныпи.м коэффициентом усиления, чем без автоколебаний, что может в известных случаях отрицательно сказаться па качестве автоматической системы в цею.м.

v=cor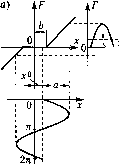

-г - 2п

б) рч = Ф(хО)

arctgfeii I О 0 \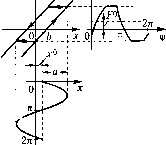