Пусть в системе (рис. 23.2, б) существует периодический режим с частотой (23.1). Положим, что па входе пелинейного звена значения и (г) изменяются по гармоническому закону:

u(i) = Asin

-г + ф

(23.21)

Тогда на его выходе получим сигнал

Uy(i) = F[u(i)] = F

Л sin

(23.22)

Один и тот же тип последовательности (23.22) может существовать при различных з]1ачепиях фазы ф сигнала (23.21). Напри.мер, если характеристика нелинейного звена идеальная релейная (см. рис. 23.4, б нри b = 0), т. е.

F[M(i)] = csignM(0,

(23.23)

то (рис. 23.6) при = 1 фаза может из.меняться от О до я, при = 2 - от О до я/2, а в общем случае

0<ф<-.

(23.24)

Последовательность (23.22) не может быть представлена рядом Фурье, как это делалось в § 18.1 для непрерывных функций. Поэто.му воспользуемся фор.мулами Бес-селя для приближеппого гармонического анализа. Выделив в получающейся при этом

тригонометрической сумме слагаемые с частотой (23.1), соответствующие первой гар-.монике, получим:

Сп . С,

22 N

u(i) = + Ci cos-г + D, sin-i. Л = 2,

(23.25)

2Л-1

с. = I .1.(0). C, = Z FLCOlcos, D,-Y (23.26)

J 2Л-1 v=0

Для си.мметричных периодических режимов (см., например, рис. 23.6) Cq = 0. В качестве примера определим коэ4)фищ1енты гар.монической линеаризации для пелинейности (23.23). В соответствии с рис. 23.6 по формула.м (23.26) находим:

С, =2с, /:>=0, Л = 1;

С, = Лдг8{п

2Л-1

Д = Лд, cos

2Л-1, 2Л

N>2,

(23.27)

2с Л

С учетом (23.27) выражения (23.25) принимают вид:

(23.28)

(23.29)

где амплитуда Л дг= СприЛ/= 1 и определяется по формуле (23.28) при Л/> 2. Следует отметить, что при Л/= 1 и Л/= 2 выражение (23.29) является точным. Из (23.21) и (23.29), используя символическую запись

w,(0 = Ave =Ае\ с учетом (23.24) опреде.чяе.м коэффициент гармонической линеаризации

q = q{A,(p,N) = --e

(23.30)

В отличие от (18.18) оп зависит не только от амплитуды Л, но и от ф и N.

Далее для определения периодических режимов можно было бы исполкювать способы, аналогичные рассмотренным в § 18.2. Однако даже вдагпюм случае при простейшей характеристике нелинейного звена этот пронесс оказывается трудое.мким. Кроме того, для других нелинейностей при получении коэффициентов гармонической линеаризации возникают большие сложности.

В.месте с тем в ряде случаев исследование периодических режи.мов можно произвести более просты.м способом.

Пусть, [гапример, характеристика нелинейного звена и.меет вид (23.23). Будем ис-полюовать нсевдочастоту Л (14.100), значе1П1Я которой на фиксированных час готах (23.1)

, 2 аг 2 п

(23.31)

Так как па входе линейной части (см. рис. 23,2, б) действует гармоническая последовательность (23.29), то нри отсутствии задающего воздействия х (г) -у (г) и на входе нелинейного звена образуется сигнал

(23.32)

где W(yA.) - частотная передаточная функция линейной части (23.8), а \\f(k) - ее аргумент.

Фазовый сдвиг на величину л вносится сравнивающим устройством. Сопоставив (23.32) с(23.21) сразу получим :

A = A,W{M, (23.33)

- + 1/(Лд,) + Л.

Так как фаза ф может изменяться в пределах (23.24) то

-<\;(А.д,)<-л+-

(23.34)

(23.35)

2N 2N

Из (23.35) следует, что периодический режим cN>2 может супюствовать, если

ЛФХ W(jX) на фиксированных частотах А.\-заходит в сектор с углом

раствора ~yv

(рис. 23.7, а). Для режима Я = 1 псевдочастота Xf =°°. Следовательгго, он воз.можен, ес;1и \W(j<)\4tO, т. е, если АФХ заканчивается на оси абсцисс.
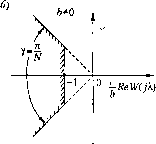