считываем всю систему в целом, как линейную, но любым обычным методам теории автоматического управления. При этом пе обращаем уже внимания па автоколебания, которые локализуются в рассчитанном ранее внутреннем контуре системы. Однако их влияние не игнорируется, ибо оно было учтено при определении функции сменюния Ф (х ) и коэффицнента

Изложенный принцип позволяет, во-первых, вести расчет автоколебаний по более простым уравнениям (так как выделяется только внутренняя часть систе.мы) и, во-вторых, значительно упрощает расчет всей системы в целом, сводя его к исследованию обыкновенных линейных уравнений (по с коэффиниепто.м зависящим от автоколебаний, т. е, от параметров внутреннего контура системы). Если необходимо учесть переменные коэффициенты и нелинейности самого са.молета, то уравнения системы в целом не будут уже столь простыми. Однако и в этом случае полностью сохраняет смысл предварительный отдельный расчет впутренпего контура системы, так как вли-я[те нелинейностей са.мого са.молетабудет распространяться об[)1чно только нате процессы движения, которые по сравнению с автоколебаниями внутреннего контура являются медчеппыми.

Известно, что и само движение самолета, например по тангажу, можно, ра.зделить на два, одно более быстрое - движение относительно центра масс (угловое Д1щжение) и другое более .медле1щое движение центра .масс (движение 1Ю траектории). Оба они являются .медленными по срав)!епию с автоколебаниями внутреннего контура систе.мы управления. Однако их тоже можно рассматривать отдельно. Следовательно, в этом случае, кро.ме обычно применяемого пространственного разбиения движения самолета но каначам (тангажа, курса, крена), расчет систе.мы по каждо.му каналу (например, тангажа) разбивается еще )1атри этапа по степени медленности движения во времещг

Аналогичное разделение расчета по крайней .мере на два этапа по степени .медленности во времени бывает целесообраз)1ым и для многих других нелинейных авто.матических систем (слежения, стабилизации и т. п.). В сложных систе.мах такие приемы, существенно упрошаюнше все исследование, оказываются единствепны.ми, которые .могут сделать расчет системы практически осунюствимым. Важно н.меть в виду, что при .это.м принципе разделения движений сохраняется существенная 11елинейна51 взаимосвязь между ними.

§ 19.3. Гармоническая линеаризация нелинейностей при несимметричных колебаниях

в главе 18 гар.моническая линеаризация пелипейностсй выполнялась для случая симметричных колебаний в систе.ме. Для гармонической линеари.зации нелинейной функции F(x,px) при несимметричных колебаниях будем полагать, что входная величинах нелинейного звена ищется в виде

х= x + asini/.

Нелинейная функция F{x,px) будет в этом случае периодической функцией аргумента Х; с П0СТ0ЯН1ЮЙ составляющей F °.

Релейная характеристика общего вида.

Релейная характеристика общего вида при несимметричных колебаниях входной величины X представлена на

рис. 19.10, а. Здесь т - любое чисю в интервале -1 2 1.

Определим постоянную составляюп1ую и коэффициенты гармонической линеаризации при условии a>h + \x\. В со-ответствии с видом функции/ (х + Gsin V), пред-ставле1Шойнарис. 19.10,6, получим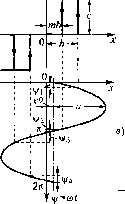

2,4/3

2л \>=<Л1

Vi = arcs)n д , v;2= arcsin - - 4,3= arcsin arcsin

b+x.

b-xO

Рис. 19.10

F- f(x +asinv/)<iy = 2л: i

С учетом значений соответствующих углов

. Z + x . /;-х . mZ + x . тЬ~хЧ

arcsm--arcsm-+ arcsm--arcsin-

a a a J

(19.74)

Далее для q (a, x ) получаем

q = - fF(x + asinv(r)siny(iy = na i

211-4,4

sm\\fd\\f- j sin\d\\f

я+4,3

--(cosy, +cosy2 +cosy.j -fcosy). na

q= - na

Учитывая значение углов у ..., 4/4, находим

,.0 ч2

.0\2

(тЬ-х)

(19.7,5)

приа> Ь + \х \.

Наконец, для q (я, х ) будем иметь

, 1

fCx +asin\j/)cosv;(iv; =sim;2 -sinv/i +sinv;4 -sinvi/..

С учетом значений соответствуюптх синусов получим

, 2сЬ,. . , 1 п 1

q=-j{-m) при a>b + \x\. па

(19.76)

Релейная характеристика с гистерезисной петлей. Считая, что релейная характеристика с гистерезисной петлей (рис. 19.10) есть частный случай релейной характеристики обндего вида при от = -1, получим

-о с

arcsm-

Ь + х

--arcsin-

. Ь-х

, 4сЬ

(19.77)

при а> Ь + \х\.

Релейная характеристика с зоной нечувствительности. Релейную характеристику с 301ЮЙ ггечувствительиости (рис. 19.10, г) следует рассматривать как частный случай релейной характеристики общего вида при т = 1. Тогда получи.м значения постоянной составляюн1ей и коэффициентов гармонической линеаризации:

. h + x . Ь-х arcsm---arcsm-

{Ь-х)

(19.78)

нри а> Ь + \х\.