ветви ВО параболы ВОВ, при М = - М. Поэтому если линией переключения сделать кривую АОВ, то при любом начальном состоянии в оптимальном процессе будет не более одного переключения. Наиример, если начальному состоян1[ю соответствует точка D с координатами Yo >0. Yo >0,товпачаяе(см. рис. 24.2) М=-М() и процесс идет по параболе DD,. В точке D, (что соответствует моменту временив, иарис. 24.2) происходит переключение паЛ7= -i-Mq и движе}1ие продолжается по линии переключения.

Для формирования алгоритма управлепия найдем уравнение линии переключения. И.ч уравнений (24.74) и (24.75) следует, что для ветви АО - 2eoY = О fipn у < О , а для ветви ВО у--2еоУ = 0 при у >0 . Таким образом, для всей линии переключения можнозанисать:

м, =f+2eoYsignY = 0. (24.76)

Правее линии переключения м, > О н М = -Mq, а левее ее м, < О и М = +Mq. В результате оптимальный по быстродействтио алгоритм управления объектом (24.69) при заданных граничных условиях можно представить в виде

M(Y,Y) = -MosignM,. (24.77)

Для реализации алгоритма (24.77) в системе используются датчик угла и датчик угловой скорости (ДУС), которые измеряют фактические значения угла у и угловой скорости у . Управляющее устройство формирует (вычисляет) значением, (24.76) и в зависи.мости от его знака осуществляет исрсключенис исполнительных устройств (например, реактивных двигателей) в соответствии с (24.77).

Следует от.метить, что реально после переключения изображающая точка будет двигаться пе но линии переключения, а несколько левее кривой АО или несколько правее кривой ВО. Это связано с тем, что иа самой линии персключеиия согласно (24.76) м, = О, тогда как в соответствии с (24.77) знак м, должен измениться. Поэтому объект не перейдет точно в заданное конечное состояние, а будет колебаться вокруг него с иебольпюй амплитудой. Для устранения колебаний вместо идеальной характеристики (24.77) можно использовать релейную характеристику с небольшой зоной нечувствительности.

Другие примеры оптиматьных по быстродействию систем приведены в работе [65 ].

П р и .м с р 3. Пусть управляемым объектом является космический аппарат, уравнепие движения которого ихкет вид (24.69), а управляюпщй мо.\[ент Мсоздается реактивными двигателями и пропорционален секундному расходу топлива, сжигаемого для образования газовой струи. Тогда функционал

/ = J M(7t = jMsignMJi (24.78)

характеризует расход топлива за время t. Требуется перевести аппарат из начатьного состояния у(0) = Уо >0, у(0) = 0 в конечное состояние у(Гк) = 0- у(к) = Отак, чтобы расход топлива был минимальным. На момент накладывается ограт[ичение М < Mq-Время разворота t., очевидно, должно быть ограничепным, но обязательно Г, > Т ,; , где min ~ время при оптимальном по быстродействию управлении.

Формируем функцию (24.59):

(\j/,x,M) = -Msign М + - ¥\М.

(24.79)

где матрицы А i\ b имеют вид (24.70). В (24.79) от управления М;?ависит только су.мма

-Msign М + \j/M = -M(sign М - b ф).

(24.80)

Пусть b \\1>1 .Тогда сумма (24.80) всегда больше ну.тя и макси.ма.тьпа при М= +М . При йф<-1 она всегда меньше пуля и максимальна при М =-Мд. Если же Ь\ <1, то .эта сумма всегда меньше нуля при любых значениях М, кро.ме М = 0. Следовательно, ее макси.мум имеет место ири М= 0. В результате получаем следующее онти.ма,тьиое по расходу тогглива управление:

М(0 =

MQsignb\\i при

при ЬЦ1 <1.

(24.81)

и пе

Уравнение (24.60) и.меет вид (24.68) и (24.71), так как функция /q(x,M) = М

зависит от X. Поэто.му, как и в предыдущем примере, 6 ij? = С, - Ct и может изменять свой знак ие более одного раза. 11о теперь в соответствии с (24,81) в оптима.льном процессе будет не более двух переключепий: с М = -Mq иа М = О, а затем с М = О на М +М() (рис. 24.4, а). Экономия топлива достигается за счет того, что на иптерва.те от t. до t2 двигатели выключены. Опти.малыгая фазовая траектория изображена на рис. 24.4, б. Пунктирными кривыми показана траектория для оптимальной по быстродействию системы.

В отличие от оптимального по быстродействию управления здесь вре.мя завершения процесса должно быть установлено заранее, ггриче.м > 7n,j . Для за,ааипых граничных условий из (24.73) найдем:

Т =2 1

(24.82)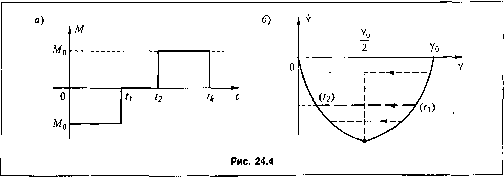

Решив уравнение (24.3) при оптимальном управле1И1и (рис. 24.4, а), получим:

2 V

4 ео

(24.83)

24 г, Расход топлива за время процесса управления 1

или с учетом (24.83) или (24.82)

Q = ?(k-VfK-/;nin).

(24.84)

(24.85)

(24.86)

где q - секундный расход топлива.

Из (24.86) следует, что при t, расход Q О , а при = Г ,( он максимален:

Qmax ?iiin-

Из (24.86) и (24.87) получим:

Г2. inin

(24.87)

(24.88)

Численно выражение (24.88) представлено в табл. 24.1, из которой видно, что заметную экономию топлива можно обеспечить при незначительном увеличении ty. но сравнению с 7j in. Эти данные .можно использовать для выбора требуемого значения г.