-180°

/ = 0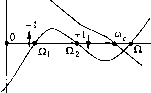

-180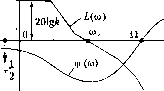

-180

3 0) о

Рис. 6.19

/ = 0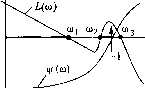

На рнс. 6.19, б изображены л. ч. х., соответствующие второй из а. ф. х., показанных на рис. 6.16. В этом случае замкнутая система устойчива, так как при / = 1 и.меется --/2 перехода через критический отрезок на частоте со = 0. Его }1аличие объясняется тем, что фаза v/ (0) = -180°, а первая асимптота л. а. х. идет параллельно оси абсцисс, т. е. .модуль А (0) = к. Это означает, что а. ф. х. (см. рис. 6.16) при со = О начинается на критическом отрезке. Иа рис. 6.19, а такого перехода пет, так как фаза 4/(0) = -180°, но первая асимптота л. а. х. имеет отрицательный наклон и Л(0) = .

На рис. 6.19, в изображены л. ч. х., соответствующие рис. 6.12. .Здесь имеется +1 переход }га частоте Q2 и -1 переход на частоте За.мк11утая систе.ма устойчива, так как /= О и сумма переходов равна нулю.

На рис. 6.19, г показан случай, когда критический отрезок состоит из двух частей. Одна его часть находится на частотах со < со а другая на частотах со3. Так как и.меется -1 переход через вторую часть критического отрезка, то замкнутая система неустойчива.

Большое практическое преимущество критерия Найквиста состоит в том, что а. ф. X. или л. ч. X. разо.мкнутой систе.мы могут быть получены ие только расчетным путем (в том числе и с иснользовапием средств вычислительной техники) ири заданной передаточной функщш разомкнутой системы, но и сняты экспери.менталыю при наличии уже созданных автоматической системы в целом или отдельных ее устройств. Это особенно важно тогда, когда достоверность исходных дифференциальных уравнений ио тем или иным причинам вызывает со.мнение.

§ 6.6. Устойчивость систем с запаздыванием

Системы с запаздыванием (см. § 1.2) отличаются от рассмотренных ранее систе.м те.м, что в одно.м или нескольких из своих звеньев и.меют запаздывание во времени начала изменения выходной величины (после начала изменения входной) на величину т, называемую временем запаздывания, причем это время запаздывания остается постоянным и во всем последуюпюм ходе процесса.

Например, если звено описывается уравнением

7-+ Х2=/.г,

(6.30)

(апериодическое звено первого порядка), то уравнение соответствующего звена с запаздыванием будет иметь вид

(6.31)

(апериодическое звено первого порядка с запаздыванием). Такого вида уравнения называются уравнениями с заназдывающи.м аргументом.

Обозначим Xi(t) = Xi(t-x). Тогда уравпение (6.31) запишется в обыкновенпом виде:

1-.Х2=Ь;.

(6.32)

Так, если входная величинах, изменяется скачком от нуля до единицы (рис. 6,20, а), то из.менение величины х,*() = х,(-т), стоящей в правой части уравнении звена,

изобразится графиком рис. 6.20, б (скачок пат секунд позже). Используя теперь переходную характеристику обыкновенного апериодического звена в применении к уравнению (6.32), получаем изменение выходной вели-чтил Х2 в виде графика рис. 6.20, в. Это и будет переходная характеристика апериодического звена первого порядка с запаздыванием (его апериодическое инерционное свойство определяется постоянной времени Г, а запаздывание - величиной т).

В обп1ем случае, как и для (6.31), уравнение динамики любого звена с запаздыванием можно разбить па два:

С{р)х2 = В{р)х\; x\{t) = x{l-x),

(6.33)

что соответствует условной разбивке звена с запаздыванием (рис. 6.21, а) на два; обыкновенное .звено того же порядка и с теми же коэффициентами и предпюствующий ему элемент запаздывания (рие 6.21,6).

Рис, 6.21

б) .Iff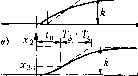

Рис. 6.22

Временная характеристика любого звеиа с запазлыва1гие.м будет, следовательно, такая же, как у соответствуюи1его обьисновениого звеиа, ио только сдвинута по оси вре.мени вправо па величину т.

При.мером звеиа чистого запаздывания т является акустическая линия связи (т - вре.мя прохождения звука). Другими примерами .могут служить система автоматического дозирова1гия какого-либо вещества, перемеп1аемого с иомоп1ыо ленточного транспортера (т - вре.мя движения лепты на определенном участке), а также систе.ма управления толщиной прокатывае.мого металла, где т означает время движения .металла от валко до из.мерителя толщины. В двух последних ири.мерах величина т называется трапсиортным запаздыванием.

В перво.м приближении определенпой величиной -запаздывания т могут быть охарактеризованы трубопроводы или дли1И1Ые электрические липни, входяпи1е в .звенья системы.

Величину заиа.здываиия т в звене можно определить экснерименталыю путем снятия премегнюй характеристики. Например, если при подаче на вход звена скач-ко.м ггекоторой величины, принимаемой за единицу, гга выходе получается экспериментальная кривая для .Tj, показанная па рис. 6.22, б, то можно приближенно описать .это звено как апериодическое звено первого порядка с запаздыванием (6.31), в.зяв величины т, Ги /г с экспери.ментальной кривой (рис, 6,22, б).

За.мети.м также, что такая же экспери.ментальпая кривая согласно графику 1)ис. 6.22, в может трактоваться и как временная характеристика обыкновенного апериодического звена второго порядка с уравнением

(7f+ Tip + 1).г2 = 0\р + ЩТ, р + \)х, = кх

(6.34)

причем Г и к можно вычислить из соотношений, записаиных в § 4.,5 для данного :вена, по некоторым замера.м на экспериментальной кривой или другими способами.

Итак, с точки зрения временной характеристики реальное звено, ириб-тижепно описываемое уравпение.м первого порядка с запаздывающи.м аргументом (6.31), часто может быть с такой же степенью приближения описано обыкновенным диффе-