
 |
|
|
Главная -> Повышение запаса устойчивости А = М\\х-х\Щх~х\= I \x--x\P-. (11.8) i = l Заметим, что без знака абсолютного значения было бы x-x-x-x = Q. Для рассмотренного выше при.мера бросания игральной кости A = xj-:fPj=-fl6-3,5 + !5-3,5 + 4-3,5! + .3-3,.5 + 2-3,5 + 1-3,5!] = . =-(2,5 + 1,5 + 0,5 + 0,5-ь1,5 + 2,5) = 1,.5. 6 Среднее отклонение случайной величины является уже не случайной величиной, а обычным числом. Дисперсией называется средний квадрат отклонения случайной величины от ее среднего значения. Она совпадает с центральным моменто.м второго порядка: D=M[{x-xf\={x-xf = {x. -xfPi. (11.9) /=1 Дисперсия .может быть легко вычислена на основании свойства среднего значения: D={x-xy- {х -2хх {хУ )=х-2хх + {xf =х- 2(х)+(ху =х-(х)\ т. е. она равна разности среднего квадрата и квадратареднего значения с.тучайной величины. Так как всегда выполняется неравенство х > {х)~, то дисперсия может быть только положительны.м число.м: D > 0. Корень квадратный из диснерсии пa:ывaeтcя среднеквадратичным отклонением случайной величины от среднего значения: а = = x-{xf. Для рассмотренного выше примера бросания игральной кости D = f{Xi-x)Pi=U{G-3,5) +(5 - 3,5)4 (4 - 3,5) + /и 6 +(3 - 3,5)2 + (2-3,5)4 (1 - 3,5)2 ] = II = 2. Средним отклонением А называется среднее значение (математическое ожидание) абсолютной величины отклонения, т. е. 298 Непрерывные линейные системы автоматического управления Среднеквадратичное отклонение a = VD = J = l,7. V12 Укажем простейшие свойства среднеквадратичных отклонений. 1. При сложении независп.мых случайных величин u = x + y + z + ... дисперсии складываются: D = D, + D, + D, + ... Поэтому среднеквадратичное отклонение суммы независимых случайных вели- Эта формула часто применяется в измерительной технике и в автоматике для вычисления среднеквадратичных ошибок. 2. Пусть имеется п случайных величин С одинаковыми средними значениями х и с одинаковыми законами распределения. Тогда их среднее арифметическое Х;+Х2+... + Х тоже будет случайной величиной с тем же самым средним значением = х , но среднеквадратичное отклонение его будет в л/й раз меньше, чем для каждой из составляющих (в случае независимых случайных величин): Например, если производится п измерений одной и той же физической величины, то их среднее арифметическое хотя тоже является случайной величиной, но всегда надежнее (имеет меньшее среднеквачратичное отклонение), чем каждое измерение в отдельности. Здесь случайные ошибки измерения в известной мере компенсируются. Но надо помнить, что систематические ошибки приборов при этом остаются в полной мере в составе среднего арифметического и никакой .массовостью измерений скомпенсированы быть не могут. 3. Для п случайных величин, не:эависи.мых и имеющих одно и то же среднее значение X, среднее арифметическое будет при достаточно болыпом п как угодно мало отличаться от среднего значения х (с вероятностью, как угодно близкой к единице). Замечание в скобках означает, что это практически достоверно, по не абсолютно, потому что средггее ариф.метическое есть все же случайная величина. Таким образом, при большом п и указанных условиях x, +Х2 + ... + Х П X ггри п- °°. 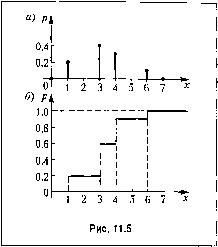 Этот закон больших чисел, доказанный П. Л. Чебышевым, имеет ггервостепенное значение для обработки экспериментальггых данных и для учетной статистики. Введем теперь порштие интегрального закона распределения. Интегральным законом распределения или функцией распределения называется вероятность того, что случайная величина примет значение, менынее некоторого значения х. Математически эта формулировка записывается в виде f(x) = P(<x), где Ъ, - текущее значение случайной величины х. Например, если график закона распределения дискретной случайной величины X имеет вид, 1юказанньш гга рис. 11.5, а, то график функции распределения для нее будет и.меть вид, показанный на рис. И.5, 6. Он показывает, что вероятность того, что величинах получит значение меньпге единицы, равгга нулю; меньше трех - равна 0,2; меггьше четырех - равна 0,6 и т. д. Функция распределения F{x) всегда возрастает с увеличеггис.м х, причем = 1 при наибольшем возможном значении х и остается равной единице при всех значеггиях х > х ,- Например, для закона Пуассона (11.3), когда дискретная случайная величина может принимать значения х = О, 1, 2, 3,..., функция распределения F{x) = YP{x) (11.10) будет и.меть вид бескопеч1гойлестниг1ы (рис. 11.6), но не .заходящей выше единицы, т. е. F(x)-> 1 прих-оо. Вероятностные характеристики непрерывных случайных величин. Неггрерывная случайная величина .может принимать все значения в каком-либо заданном ограниченно.м интервале (а < х < й) или все значения от -оо до -Ноо. Следовательно, функция распределения (интегральный закон распределергия) для неггрерывной случайной величины будет изображаться непрерывной кривой. На рис. 11.7 показаны оба упомянутых выше варианта. Вероятность 2 4 6 8 10 12 Рис. 11,6
|