Уравнение объекта (24.8) ириводится к виду (24.3) ири А = --, h = - .C учетом

о о

функционала (24.19) составляем функнию (24.59):

Я = -(л- - Xq f + pw4 Arv + bMfu. (24.61)

Так как на унравленне и ограничение не накладывалось, максимум Я определяем в соответствии с (24.58):

Таки.м образом, опти.мальное управление

= -2р M + iv/ = 0. (24.62)

h\\i

Уравнение (24.60) имеет вид

7- (24.63)

д г, .9 2 2

(х-ХоУ+\хи -А\]1 = 2(х-х(,)-А\\1. (24.64)

Отсюда находим:

2(.г-х )2о(х-х ) 24.65)

р + Л ар-а

При v/ = аХ выражения (24.63) и (24.65) совпадают с (24.23) и (24.24). Поэтому далее задача решается точно так же, как в § 24.2.

П р и м е р 2. Пусть объект задан уравнением (24.3). На управление наложено ограничение и < {/ . Требуется найти управление, которое переводит обт>ект из состояния х(0) в состояние x{t) .за минимально возможное вре.мя = 7, i .

В§24.1.огмеча.,тось,что при onTHMajnioM ио быстродействию управлении в функционале (24.55)/о = 1. Тогда функция (24.59)

Я(ф,х,м) = -1 + хАЩ + Рщ. (24.66)

В (24.66) от управления зависит только слагаемое . Поэтому Я принимает максимальное значение по и только тогда, когда максимальной является величина . Очевидно, что это имеет место при w = -i-t/, если йф>0,им = - и,если Ь <0. Таким образо.м оптимальное управление

u = UsignP\. (24.67)

Следовательно, оптимальная ио быстродействию систе.ма всегда будет релейной, но не обычной релейной, а с особым законом переключения реле по знаку вспомогательной функции foij?.

Уравнение (24.60) при /д = 1

lj/ = -А Ц1.

(24.68)

Его рей1ение (см. гл, 5)

ф(0 = е- Ф(О).

Но так как начальное значение \j/(0) не задано, то можно найти лить общий вид вспо.могательной функции vj/(0

Несмотря па это задача синтеза опти.мального управлепия .может быть решена до конца.

Рассмотрим теперь кощ<ретную задачу. Пусть управляемым объектом является космический аппарат. Уравнение его движения относительно продольной оси и.меет вид

у = е, е = -, J

(24.69)

где у - угол крена, М - управляющий мо.мент,/ - момент инерции.

На величину управляющего момента наложено ограничение \М\ < Мд . Поэтому ограничивается и ускорение: £ Eq . Требуется перевести аппарат из произвольного начального состояния в конечное состояние y(t) = О, у(г) = О за миии.мальное время t = Т

к Iran-

Обозначи.м Xj = у; 2 = у, и = М . Уравнение (24.69) приведем к виду (24.3), где

(24.70)

Получаем уравнение (24.68):

(24.71)

Из пего находим: v/, = С v/2 =с2-C,t, b\i = \\i2. Определяем оптимальное управление (24.67):

M = Mosign (с2-С,0.

(24.72)

1 [оскольку функция С2 - Ct .может и.змспять свой знак не более одного раза, то в оптимальном процессе будет пе более одного переключения с М = па М = -Л/ц или наоборот.

Пусть, напри.мер, в начальном состоянии у(0)=Уо >0, у(0) = Уо > О . Тогда, очевидно, наперво.ч[ ипгервале необходимо иметь М = -Мо(рис. 24.2, я). В некоторый niomcht времени t = t, должно произойти переключение па М = +Mq, а при t > t,. у1[равление

tk t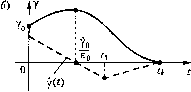

Рис. 24.2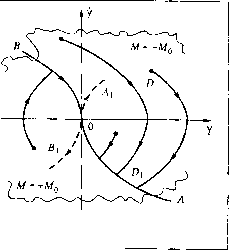

Рис. 24.3

М = 0. Решив ири этих условиях уравнение (24.3), нолучим оптимальную траекторию (рис. 24.2, б) и выражения

к-Лшп- -+ 2-J + --, 1- + -

(24.73)

Используя (24.73) можно реализовать оптим;иП)Пое управление как функцию времени: Л/= iU(0.

Для получения оптимального управления как фупк1и1и переменных состояния у и Y изобразим процесс на фа.эовой плоскости (рис. 24.3).

Исключив из уравнения (24.69) dt, как это делалось в главе 17, получи.м при М = -t-iUo дифференциальное уравнение

ydy = £ody,

откуда после интегрирования найдем уравнение фазовых траекторий

Аналогично при М= -Mq имеем

(24.74)

(24.75)

Таким образом, фазовые траектории представляют собой параболы, сим.метрич-ные относительно оси абсцисс.

При М= +Mq они обрапгены вершинами влево, а при Л/ = -М - верпнигами в[[раво.

В заданное конечное состояние y(t) = О, y(t) = (),T. е. в начало координат, изображающая точка может попасть лишь по ветви АО параболы ЛОЛ) при М = +Mq или по