а f{w) - нелинейная функция, например, вида рис. 17.14, б. Введе.м обозначения переменных:

-г,--5, х,-, X;j=pvi;.

Тогда уравнения автопилота (17.72) и самолета (17.55) примут вид (17.71), а и.менно:

pxi =-k,x -крЪ -Р{Х2),

р.Г2 =Xj, k 1

(17.73)

Зададимся функцией Ув виде

y = \b\xi +b2xl +633 +1212 +1313 +2323-

где все шесть коэффициентов й пеи: *естны. Потребуем, чтобы функция

dV dV dV

= 3- рл-, + -- ;JX2 + - /JX3

при фиксированном значении F{x,) = 0x2 в уравнениях (17.73) имела вид

W,=-{x+xl+xl).

(17.74)

(17.7.5)

Тогда путем приравгтвания соответствующих коэффициентов выражений (17.74) и (17.75) можно найти все шест ь величин h из системы шести алгебраических уравнении. Здесь приводится результат решения только для трех коэффициентов, которые понадобятся в дальнейшем, а h.vichho:

- D,

(17.76)

D, = a,k, (Щ +k,) + (Г, V + l)( o + ). Аз =?iK)(7i o +

Затем потребуем, чтобы выражение (17.74) при замене в уравнениях (17.73) F{X2) = 0X2, где я = Яр + Ля, имело вид

W = -(Ci xl + С2 х + Cg х +2 С,2Х,Х2 + 2 C,3X,X.j +2 С23Х2Х3),

что дает значения:

С] =Сз =1, С2 =6,2Ля + 1,

2с,2=-6,Ла, 2с,з=0, 2с2з=6,зЛа.

(17.78)

Функция ТУбудет знакоопределенной отрицательной, как требуется по условию, если

С2 > О, С2С3 - С.23 > О, С, С2С3 + 2 С, 2С,зС2з - С, С23 - cfy - С3 Ci2 > 0.

Эти неравенства с учетом (17.78) приводятся к следующему:

Подставив сюда (17.76), увиди.м, что это условие выполняется, если Да лежит в интервале Ля, < Ля < Ая2 где

А и =~m4D+b( + Dl,), (17,79)

откуда видно, что Ая, < О и Ля2 > 0. При этом требуется еще D>0. Нетрудно проверить, что последнее требование совпадает с критерием устойчивости (см. § 6.2) для данной системы в линеаризованно.м виде при замене F(vj/) = Я()\/ (рис. 17.14, б), так как характеристическое уравнение согласно (17.55) и (17.72) в .этом случае будет

l]p+(TAc+np+ik +kk,)p + a,k,=0. (17.80)

Итак, для устойчивости рассматривае.мой нелинейной системы достаточно, во-первых, чтобы выполнялся критерий устойчивости Гурвица D > О для линеаризованной системы при F(\/) = Яо\/ и, во-вторых, чтобы нелинейная характеристика F(\\i), измерителя управляемой величины лежала, как указано па рис. 17.14, б, между пря.мыми f = я,\/ и f = Я2\/, причем а, = о + Ля 2 = Яр -ь Ля2, где значения Ля, 2 определяются формулой (17.79), в которой величины D, D 0,3 согласно (17.77) выражаются через параметр>1 данной системы и через первоначально принятое значение при линеаризации F(\j/) =aoVj/.

Как и в предыдущем примере, здесь получаются условия абсолютной устойчивости, т. е. условия, не зависящие от формы нелинейности, но в более узких, чем (17.54), пределах, показанных на рис, 17.14, б. Точные аналитические методы исследования релейных систем рассмотрены в работах [ 67,89,95 ] и др.

Q(p)=ciqp +ар ~ +... + а р + а , R{p) = h,p +h,p -+... + h ,p + h

причем будем считать т<п.

Пусть }1елинейпость у = F(x) имеет любое очертание, пе выходяп1ее за пределы заданного угла arctg (рис. 17.15, б), т е, при любом х

0<F(x)<k,.x. (17.83)

Пусть многочлен Q (р) или, что то же, характеристическое уравнение линейной части Q (р) = О имеет все корни с отрицательны.ми вещественными частями или же кроме них имеется enie не более двух нулевых корней. Другими словами, допускается, чтобы а = О пли а = О и а ] = О в выражении Q(р), т. е. не более двух нулевых полюсов в передаточной функции линейной части системы

Rjp) Qip)

Приведем без дока.зательства формулировку теоремы В. .М. Попова: для установления устойчивости нелинейной системы достаточно подобрать такое конечное действительное число h, при котором при схсо > О,

Re(l + /(oA)U(jft))]+-->0, (17.84).

Линейная г часть п

Пелиней-

ность

Urctg kf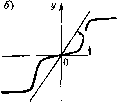

Рис. 17.15

§ 17.3. Частотный метод В. М. Попова

Решение задачи об абсолютной устойчивости системы с одной однозначной нелинейностью (т. е. устойчивости ири любой форме этой нелинейности со слабым ограничением тина (17.54) или тина рис. 17,14) с помошью теорем прямого метода Ляпунова было проиллюстрировано на двух при.мерах в § 17.2.

Изложи.м теперь частотный метод, предложенный ру.мынским ученым В, М, Поповым [69], ири использовании которого та же задача решается более просто приемами, апалогичиы.\и1 частотным способам исследования устойчивости линейных систе.м.

Если в системе авто.матического управления имеется лишь одна однозначная нелинейность

y = F{x), (17.81)

то, обТ)едипив вместе все (;стальные (линейные) уравнения системы, можно всегда получить общее уравнение линей}Н)й части систе.мы (рис. 17.15, а) к виде

Q{p)x = -R(p)y, (17.82)