в:,-2=ь1

Ь а

k % )

b -2 а ~1 bo йо

I о j

*о йо j

й-4

1*0 йо j

B\ = bl

bo 0;

b a

1*0 0

b ~i = *o

I bo 0

(8.66)

При иостуилении на вход системы единичного и.миульса 5(Г) = Y {t), изображение которого но Лапласу равно 1, изображение управляемой величины можно также представить в виде дробно-рациональной функции (8.60). Разница будет заключаться только в том, что степень числителя т возрастает на единицу, а последний коэффициент числителя = 0. Это обусловлено те.м, что получение реакции систе.мы па единичный импульс (весовой функщи) эквивалентно дифференцированию переходной функции, получающейся при действии единичного скачка. В области изображений это эквивалентно умножению на комплексную величину р.

В связи с этим квадратичную интегральную оценку при действии единичного импульса .можно рассматривать в виде выражения

(8.67)

где ж(г) - весовая функция системы но задающему или возмущающему во.здействию, x{t) - отклонение управляемой величины от нового установивпгегося состояния в переходпо.м процессе при действии едигшчпой ступеньки задающего или возмуща-юпюго воздействия.

Таким образо.м, техника вычисления оце1и<и / полностью совпадает с вычислением оценки / но формуле (8.61) или (8.65). Совпадает при этом и значение определителя Д (8.62). Отличаться в вычислениях будут определители До, А, и козф-

фшшстъ1Во,...,В или В, В , что обусловлено повьннением степени тввыра-жении (8.60) на единицу при вычислении / по сравнению со случае.м вычисления /.

Интегральная оценка / также может использоваться в безраз.мериом виде аналогично формуле (8.57):

4=-- (8.68)

Интегральные оценки In Г (или выражения квадратичных динамических ошибок) применяются для выбора структуры и параметров систем автоматического управления. При это.м наилучшими гшра.метрами считаются такие, при которых величина I или / имеет минимальное значение. Вычисление квадратичных тггеграль-

ных оценок / и / можно также производить иа основании так называемой формулы Релея, которая будет дока,запа ниже, в главе 11, Здесь она будет приведена без доказательства.

Если X(j(}}) есть изображение Фурье функции времени x(t), то существует зависимость, определяемая теоремой Парсеваля

]x\t)clt =j-]\X(Mf rfw=i ]X(7C0)f clay,

т. е. интегрирование квадрата функции но времени в пределах от пуля до бесконечности можно за.мепить интегрированием квадрата модуля изображения Фурье этой функции по всем частотам. При нахождении интегральной оценки /, соответствую-Н1ей peaKiuiH системы на входное задающее воздействие типа 1(f), изображение Фурье исследуемого отклонения х(С) = г/(°°)У(0 будет

где Ф(/со) - частотная передаточная функция замкнутой системы. Тогда

, ГгФ(0)-Ф(7Со)- ,

/ = -[ со. (8.69)

Л (if

В астатических системах и статических системах с пеедипичпой обратной связью или с масштабированием (см, § 9.3) установившееся значение у (°°) = 1 и Ф (0) = 1. Тогда формула (8.69) будет иметь вид

1=-]-Щ- dbx (8.70)

где Ф.(;(й) = 1 - ФОсо) - частотная передаточная функция замкнутой системы по ошибке.

Аналогичным обра;юм для входного задающего воздействия типа единичного импульса 5(f), изображение которого равно 1, изображение Фурье исследуемого откло-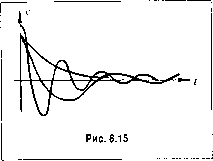

нения х(0 = -y{t) равно частотной передаточной функции за.мкнутой систе.мы: X(j(a) = = Ф(/со) 1. В резу;нугате получаем

r = i Ф(;со)(о. (8.71)

Подобные выражения могут быть нолучетш! и для входного возмущающего воздействия, если вместо частотной передаточной функции Ф(/со) использовать передаточную функцию по возмущающему во.эдействию Ф (;(0), Недостатком интегральных оценок является то, что здесь ничем не ограничивается форма кривой переходного процесса. Оказывается, например, что три совершенно различных но форме процесса, изображешгых па рис. 8.15, имеют одно и то же значение квадратичной интегральной оценки (8.56). Часто оказывается, что выбранные по минимуму этой оценки пара.метры сисгемы соответствуют сильно колебательному процессу, ибо отмечавшееся уже при это.м стремление приблизить процесс к идеальному скачку вызывает большую скорость процесса при подходе к установивше.муся значению х = 0.

Это получается вследствие того, что оценка (8.56) учитывает только величину отклонения и быстроту затухания и никак не учитывает близость системы к колебательной границе устойчивости.

Если, например, подать на вход системы единичный скачок, то оишбка в переходно.м процессе определится заштрихованной частью на рис. 8.16, а. Очевидно, что величина интегральной оценки (8.56) будет те.м меньше, че.м ближе будет кривая переходного процесса к ломаной линии АОВС. Но приближение процесса к этой линии требует увеличения угла наклона кривой в начальной стадии процесса (приближение части кривой 0D к отрезку ОБ).

Увеличение же пача-аьной скорости .может вызвать значительное перерегулирование и, следовате.тьпо, малый запас устойчивости.

Поэтому применяется еще другой вид интегральной оценки, в которой ограничение накладывается не только на величину отклонения х, но также и на скорость отклонения х. Эта улучшенная квадратичная интегральная оценка имеет вид

1 = 1{х-+ТЧ)Л,

(8.72)

где Г - некоторая постоянная времени.

Выясним, какой вид переходного процесса будет получаться при выборе пара.метров системы по минимуму улучшенной интегральной оценки (8.72). Для этого проделаем следуюпню преобразования:

/, = (х Txf dt - 2Гх xdt= ](х Txf dt - Тх = Txl + ](х -t- Tifdt,

ООО о ,

гдехц - начальное значение отклонения в переходном процессе.