(6.26)

Фаза (аргумент) частотной передаточной функции

\/((0) = -Г -90° + 2arcf.g(0Ty - arctgcor;.

Па основании (6.26) можно легко, без дополнительных вычислений построить аси.\нгготическ\10 л. а. х., для чего на стандартной сетке (рис. 6.18) наносятся вер-

-1 -i-

тикальные прямые при сопрягаюншх частотах - 7. и Для оирсделенно-

сти построения возьмем передаточную функцию разо.мкнутой системы

p{\+i\p)i\vi\pY (ь-)

которой соответствует выражение для модуля в логарифмическом масштабе

L(co) = 201g £5!-,

V(i+7;V)(i + 72V) (

При.мем, например, что /С = 50 с , Г, = 0,5 с, т, = 0,2 с, 7, = 0,0125 с. Тогда сопря-гаюнте частоты ю, = 2 с , = 5 с , щ = 80 с .

Вначале построим первую аси.мн готу. При со < ю, выражение (6.29) приобретает

i((o) = 20lg-, м

которо.му (см. § 4.4) соответствует пря.мая с наклс)1гом -20 дБ/дек, пересекающая ось абспнсс при 03 = tt)j, = К. Для получения второй точки этой прямой откладываем от точки =50 с одну декаду вправо, т. е. до частоты tt) = 10a)(.j =500 с , и находим точку D, находяп1уюся на 20 дБ ниже оси абсцисс. Можно отложить одну декаду и влево до частоты а) = 0,1а). =5 с и найти точку Dj, находящуюся иа 20 дБ выше оси абсцисс.

Первую асимптоту проводим до первой сопрягающей частоты о), (точка Л). Так как этой частоте соответствует постоянная времени 7 находяптаяся в знаменателе (6.28), то ;i. а. х. необходимо и,з.г10мать на -20 дБ/дек, и наклон второй асимптоты станет равным -40дБ/дек. Это означает, что через одну декаду, т. е. на частоте 03= Юоз точка/4 опустится на 40 дБ.

При подстановке р =]ш получаем

I(©) = 201g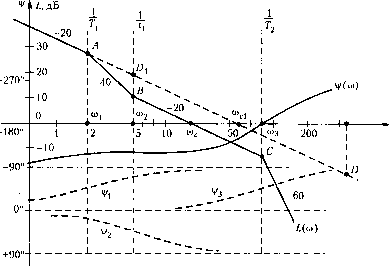

500 о),с-

Рис. 6.18

Вторую асимптоту доводим до второй сопрягающей частоты (точка В). Так как частоте ©2 соответствует постоянная времени т паходяп1аяся в чисунггеле (6.28), то л. а. x. пз-тамываем иа +20 дБ/дек и наклон третьей асимптоты составит -20 лБ/дек. Доводи.м ее до третьей сопрягающей частоты ©3 (точка С). Так как этой частоте соответствует постоянная времени 7-2 сомножителя второго порядка знаменателя (6.28), то л. а. x. и.зламываем на -40 дБ/дек и последняя acииIтoтa будет иметь наклон -60 дБ/дек.

Действителыгая л. а. х. несколько отличается от асимптотической (см. §4.,5). Максимальные отклонения имеют место на сопрягающих частотах. На частоте ©i действительная л. а. х. проходит иа 3 дБ ниже, иа частоте ©2 - на 3 дБ вьпне, а на частоте ©3 - на 6 дБ ниже аси\и1тотической.

Выражение для фазы (6.28) имеет вид

1/(©) = -90° - arctg ©Г, + arctg шт, - 2arctg ©Уз = -90° +-4/1+4/2 + 24/3. (6.30)

Каждая из составляющих ц/ ц/з, 4/3 представляет, по сути дела, одну и ту же зависимость от частоты. Поэтому достаточно построить, например, то.тько зависимость Vi = -arctg ©Г, (см. рис. 6.18). Все остальные получаются простым сдвигом этой фазовой характеристики так, чтобы иа соответствук)П1ей сопрягающей частоте иметь фазовый сдвиг 45°. При это.м необходимо учитывать знак каждого слагаемого (6.30). Логарифмическая фазовая характеристика (рис, 6.18) получается в результате алгебраического суммирования всех слагаемых (6.30). Построение л. ф. х. .можно существенно упростить, если заранее будет подготовлен nia6;ioH для одной из указанных зависимостей.

Аналогичное построение л. а. х. и л. ф. х. может быть сделано при любом значении г. Разница будет заключаться в нак;к)не первой асимптоты л. а. х. и величине первого слагаемого выражения для фазы (6.27).

При г = О первая асимптота проходит параллельтю оси абсцисс на расстоянии 20 Ig К При г > 1 ее наклон равен -г 20 дБ/дек, а ее частота среза = Vk.

В тех случаях, когда в передаточной функции разо.мкнутой системы (6.22) и.меются сомножители типа тр + 2т:р + 1 и Тр + 2Тр + 1 с комплексными корнями, построение асимптотической л. а. х. принципиально не отличается от рассмотренного выше. Сопрягающими частотами для них будут © = - и (0 = -. На первой л. а. х.

дополнительно изламывается на +40 дБ/дек, а на второй - на -40 дБ/дек. Однако при малых значениях параметра затухания отклонение действительной л. а. х. от асимптотической оказывается значительным. Поэтому при < 0,3 в асимптотическую л. а. x. следует внести поправки в соответствии с рис. 4.15 или рис. 4.16 (для первого из указанных сомножителей они берутся с обратным знаком).

Аналогично изложенному выше строится и л. ф. х. Для построения составляющих фазовой характеристики, соответствующих сомножителям с комплексны.ми корнями, можно использовать графики, приведенные на рис. 4.15.

Обратимся теперь к исследованию устойчивости замкнутой систе.мы но построенным л. а. x. и л. ф. x. разомкнутой системы. Для этого воспользуемся последней из приведенных выше формулировок критерия Найквиста, связанной с прохождением а. ф. x. через критический отрезок.

На плоскости а. ф. х. ра.зомкнугой систе.мы критический отрезок (см. рис. 6.16) представляет собой отрезок вещественной оси, на котором фа;}а i/(co) = -180°, а модуль Л(со) > 1. На плоскости л. ч. х. разомкнутой системы фаза i/(CD) = -180° на всей оси абсцисс, а модуль Л(со) > 1 там, где/.(со) = 20 Ig Л(со) > 0. Напри.мер, на рис. 6.18 эти условия вьшолняются на отрезке оси абсцисс, расположенном левее частоты среза л. а. x. ю.

Таки.м образом, для устойчивости замкнутой системы необходимо и достаточно, чтобы сумма переходов логарифмической фазовой характеристики разомкнутой системы через критический отрезок была равна -, где / - число корней с положительной вещественной частью в знаменателе передаточной функции разомкнутой системы W(p). Как и прежде, переход сверху вниз считается положительным, а снизу вверх - отрицательным.

Так, на рис. 6.18 л. ф. х. не пересекает критический отрезок (переходов нет), в знаменателе передаточной функции (6.28) корней с положительной вещественной частью нет (/ =0) и, следовательно, замкнутая система устойчива. Аня/тогично обстоит дело и с замкнутой системой, л. ч. х. которой в разомкнутом состоянии изображены на рис. 6.19, а. В обоих случаях при увеличении коэффициента передачи разо.мкнутой системы л. а. х. будет сдвигаться вправо параллельно самой себе, а л. ф. х. изменяться не будет. Поэтому (см. рис. 6.19, а), когда частота среза л. а. х. ш. станет равной частоте О., замкнутая система попадет на колебательную границу устойчивости, а при > Q появится -1 переход через критический отрезок и замкнутая система станет неустойчивой.