бениост.ь, что передаточной функцией линейной части системы (см. рис. 23.2, б) будет

Wiz) = W,(z)D(z). (23.7)

Для получения частотной передаточной функции удобно иснолыовать псевдочастоту X (14.100) иламену (14.99). Тогда

WUX) = \V,(jX)DaX) (23.8)

и условие (17.86) нри.мет вид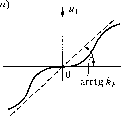

Рис. 23.4

U\X)-h,ViX) + -l->0,

U(k) = \\cW{jX), V =Xr\mW{iX),

(23.9)

(23.10)

Tq = 1 с - нормирующий .множитель, a коэффициент i/,-определяет левую границу сектора, к которому принадлежит характеристика нелинейного звена (рис, 23.4).

Если коэффициент отнести к линейной части системы, то вместо (23.9) нолучим:

kpU (X)-hkpV\X) + \>0.

(23.11)

Это означает, что для установления устойчивости системы достаточно подобрать такую прямую на нлоскости W {jX), проходящую через точку (-1;;0), чтобы вся кривая

kp W iJX) = kpU (X) + jkpV (л)

(23.12)

лежала справа от этой прямой.

Для систе.м высокого порядка значения U(X) и V(X) проще находить по известным формулам:

U(X) = A(X)cos\v(X), V(X) = (A)sin i/(X),

(23.13)

где A(X) и Ц!(Х) - модуль и аргумент частотной нередаточной функции (23.8). В этом случае кривая kpW(jX) определяется следующим образом:

kpW(jX) = kpA(X)[coii\]i(X) + jXTQsm\v{X)]. (23.14)

Пример 2. Пусть передаточная функция непрерывной части системы

P(TiP + l) Р Tip + l

(23.1.5)

персдагочггая функция дискретного корректирующего устройства D(z) 1, гюстоян-ная времени 7, = 0,2 с, период дискретности Т= 0,1 с, нелинейная характеристика релейная с зоной нечувствительности (рис. 23.4, б), с = 1, = 0,2.

Отметим, что непрерывная система с передаточной функцией линейной части (23.15) и данной характеристикой нелипейпого звена устойчива, так как характеристика

W (;а)) = -

1 + 7V l + r,W

целиком располагается в третьем ква/.1рапте плоскости W*{jm). Этот вывод совпадает с иолучепным в § 17.1 (пример 3, рис. 17.3, е).

Для исследования дискретной системы находим передаточную функцию (23.7):

U() = UV) = --2-1 Z-d

d = e

Соответствующая ей частотная передаточная функция (23.8)

1-Ь7л(Г2-Г,)]

(23.16)

T\ + d Т , Т

2 = - --Г = -Ctll-

2 1-fl 2 2Г,

При заданных значениях Г и Г, отношение 7У2Г значительно меньше единицы. Поэтому приближенгго можно принять

27, Г

7; =7,.

Тогда выражение (23.16) упрощается:

(23.17)

Отсюда с учетом (23.10) и (23.12) находим:

k,-V\X) = -kT,

(23.19)

Кривая (23.12) изображена иарис. 23.5, а. Та.м же в координатах U и Упуиктирной кривой показана АФХ приведенной линейной части системы, соответствующая (23.17), при k = kokf-OCie характеристики пересекают ось абсцисс при значении псевдочастоты

(23.20)

па расстоянии 7У2 от начала координат.

Из рис. 23.5, а видно, что достаточное условие положения равновесия выполняется при kT< 2. За.мети.м, что в данпо.м случае оно совпадает с необходимым и достаточ-пы.м условием устойчивости замкнутой линейной дискретной системы (см. гл. 14), у которой частотная передаточная функция разомкнутой систе.мы имеет вид (23.16), а коэффициент передачи k = кф.

При кТ> 2 пелипейная дискретная система может стать неустойчивой. Для подтверждения этого на рис. 23.5, б пока.зан фрагмент кривой переходного процесса, построенной аналогично тому, как .это сделано в п]5имере 1, при 7= 4,g = О и начальных условиях X (0) = 0,2; х (-1) = О, Видно, что в системе устанавливаются нериодические колебания с периодом, равпы.м 8T(N= 4), С.тедует отметить, что выполнение условия кТ< 2 ие 1-араптирует устойчивость систе.мы при наличии внешних воздействий.

Метод гармонической линеаризации при его применении для исследования нелинейных дискретных систем в значительной стеиепи утрачивает свои ценные качества. Рассмотрим основы этого .метода.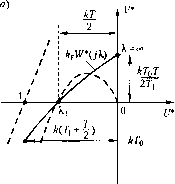

0,6 0,4

-0,2 -0,4

-0,6