§8.2. Точность в типовых режимах

Для оценки точности систе.мы управления исноль.зуется величина оитбки и различных типовых режимах. Ниже будут рассмотрены наиболее угготребительные режи.м ы.

1. Неподвижное состояние. В качестве типового режи.ма рассматривается уста-повшппееся состояние при постоянных значениях зада1оп1его и воз.мущающего воздействий. Опшбка системы в этом случае называется статической. Величина оитбки может быть найдена из общего выражения (5.6). Для этого необходн.мо положить g{t) go ° const. Далее необходн.мо учесть действуюппю гга систему воз.мущепия. В обще.м случае их может быть песколько:/](/,),/2(с) п т. д. Тогда в правой части (5.6) появится несколько слагаемых, определяемых имеющимися возмущения.мп. В неподвижном состоянии необходимо положить /[(О =/]о = const,/2(0 =/20 = const и т. д. Затем можно использовать изображения фупкпи!! по Лапласу или Карсону-Хевисайду. Используем, ггапример, изображегшя Карсона-Хевисайда. Тогда изображение постоянной величиггы равно ей самой, т. е. С(р) = gQ, Ff(j}) =/\ц,р2{р) /20 и т. д. Далее необходн.мо воспользоваться теоре.мой о конечном значении (см. табл. 7.2) и получить установившееся значение ошибки (статическую ошибку):

l + Wip)

1 W{p)

(8.1)

где / - число действующих на систему возмущений, а Wfip) = - Wj{p).

Ilei)B()e слагаемое представляет собой составляюгцую статической ошибки от задающего воздействия, а второе х - от возмущающих воздействий.

Входящая в выражение (8.1) передаточная функция paзo.vпcцyтoй системы W(j)), как показано в § 6.4, может быТь представлена в виде (6.22), где К - коэффициеггт передачи разомкнутой систе.мы, аг - число интегрирующих звеньев, входящих последовательно в разо.мкнутую цепь системы. При ?= О система называется статической, а при г> \ - астатической. Величина г определяет иоряс)окас/па?/гшла системы.

В статических системах в болыпинстве случаев W{Q) = К. Тогда статическая ошибка от задающего во,здействия

Мо

1 + W(Q) \ + К

(8.2)

Однако отсутствие зависимостей, связываюпщх в общей форме свойства системы во временном и частотном представлениях, пе может служить препятствием для развития и независимого исчюльзования критериев качества того или иного направления.

Использование того или иного подхода при формулировании критериев качества определяется в настоящее вре.мя удобствами его примеггения в системах конкретного вида, а также, в известной мере, сложившимися в дайной области традиннями.

В некоторых случаях, например, при наличии в знаменателе W(j)) сомножителя с положительным корнем, Vl(0) = -К. При этом

Составляющая онп1бкп .г практически всегда может быть сведена к нулю посредством использования неединичной обратной связи или путем маснгтабирова-ния (см. § 9.3).

В астатических сисге.мах U(0) --> Поэтому первая составляющая (8.1) обращается в нуль.

Второе слагае.мое (8.1) никогда не обращается в иу.ть, так как даже испол1)Зова-иие управления с астатизмом высокого порядка и использование принципа унравлс;-ния по возмущщгию (см. § 9.2) .могут обратить в пуль .типи) часть слагаемых, находящихся иод знаком суммы (8.1).

При выводе выражения (8.1) предполагалось, что чувствительный эле.меит, он-ределяюпцтй разггость между требуе.мых! и действительным значения.ми уи1)авляе-мой величины, является ндеальны.м и определяет имеющуюся ощибку в соответствш! с выражен нем-г (г) = g([)-- у (С). В деист вительпостн нувствительно.му .элементу как измерительио.му органу присущи свои опнтбки. Ошибку чувствительного элемента .можно рассматривать также как некоторое воз.мущающее воздействие, и считать, что она входит во второе слагаемое (8.1). Однако на практике удоб1гее.эту опнгбку учитывать отдельно и считать, что статическая ошибка равна (ири х., = 0)

-(т =<Т +ГТ (8.3)

где х . представляет собой второе слагаемое в выражении (8,1) и определяется внешними возмун1ения.ми, .г* является ошибкой чувствительного элемента.

Рассмотрим теперь ошибку x j. При,ме.\1 для простоты, что па систе.му действует одно возмущающее воздействие/j. Тогда в статической систе.ме иолучи.м

. Wi(Q)/io Yi/u. ~ l + WiQ)~l + K- (8.4)

или при Ж(0) =-/f

YiTio \-К

В этих равенствах у, представляет собой отношение установившейся ошибки к постоятю.му возмущению (коэффициент статизма) в разомкнутой системе. Эта же величина, деленная па 1 ± К, соответствует коэффициенту статизма в замкнутой системе. Величина 1 ± /f, по сути дела, показывает эффектив1Гость управления с точки зрения у.меньшепия установившейся ошибки.

В астатической системе W (0) -> °°. Однако это eni,e ие озггачает, что х О, так как возможен случай, когда (0) -> °°. Вследствие этого для каждого действующе-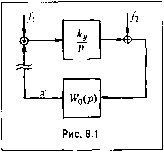

и в замкнутой

го на систему возмущения необходимо определить факт наличия или отсутствия установившейся ошибки гсо-средством нахождения значеггия (8.4).

Для иллюстрации этого на. рис. 8.1 изображена сгрук-турная схе.ма системы автоматического управления. Она содержит объект с передаточной функцией Wq (р) и астатическое управляющее устройство с передаточной функшюн Wy (р) = ky/p. Пусть объект не имеет интегрирующих свойств и Wq (0) = kfj.

На систе.му действуют два воз,\сущения -/, и/2. В разомкнутой систе.ме (как нока.запо па 1)ис. 8.1)

x = W (p)

Wo(p)

х = -

1 + W{p)

где W(p) = Wq(p) Wy(p) - пе1)едаточпая футгкция разомкнутой систе.%н.1. Отсюда по Teoj)eMe о конечном значении определяем установпв1пуюся ошибку, положив р === О, /] (О =/,0= const,/2 (О =/20 = const,

- vcT -

Кг г

~У10 +/20

\ + W{p)

Таким образом, первое возмущение дает статическую ошибку, а второе гге дает. Из рассмотрения рис. 8.1 видно, что воз.мущегше /, приложено до интегрирующего звена, а /2 - после. Из этого и вытекает правило, по которому можно определить, устраняет ли астатический алгорит.м управления статическую оин1бку от какого-либо возмуп1епия. Для выполнения этого необходн.мо, чтобы иргтегрируюингй элемент был включен в цепь управления до места приложения данного возмущения. Это объясняет, в частности, тот факт, что включение иитегрируюппьх элементов и 110выщение порядка астатиз.ма не дает возможности устранить ошибку чувствительного элемента X* , которую .можно рассматривать как воз.мущеиие

2. Движение с постоянной скоростыо. В качестве второго типового режима используется режим движения системы с постоя11Пой скоростью v const, который будет наблюдаться в установившемся состоянии при задающем воздействии, изме-пяюще.мся по закону й(г) = vt. где г;= const, и пои постоянных значениях возмущаю-