dV dV dV

-X{x,X2)+--X2{x,x2) = W{x,X2)

dt дх.

ока.залась зпакоопределенной положительной. Пусть при этом линии V{x, Х2) иа фазовой плоскости располагаются, как указано на рис. 17.11, где линии АВ и CD соответствуют значениям V= О и разделяют те области, внутри которых V> О и V< 0.

Возьмем изображающую точку М, как показано на рис. 17.11. Поскольку там V <0 и везде

то изображающая точка М с течением времени будет двигаться и пересекать линии V = С, переходя от меньших значений С к большим. Она .может при этом лишь временно приблизиться к началу координат, по в копне концов будет неограниченно удаляться от начала координат. Это соответствует расходящемуся процессу, т. е. неустойчивости системы. Аналогично .можно показать справедливость теоремы и для системы любого порядка п, проводя те же рассуждения для и-мерного фазового пространства.

Приведем два примера применения изложенных теорем Ляпунова к исследованию нелинейных систем авто.матического управления.

Пример учета нелинейности привода управляющего органа. Такой при.мер применительно к системе самолета с курсовым автопилотом (в упрощен-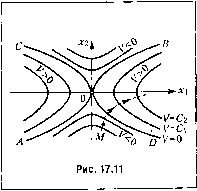

система хотя и не будет асимптотически приближаться к устанонивпгемуся состоянию, но все же будет все время в достаточной близости от него.

Теорема Ляпунова о неустойчивости нелинейных систем. Поскольку предыдущая теорема Ляпунова дает, Boo6nie говоря, только достаточные условия устойчивости и поскольку кроме области устойчивости нелинейная систе.ма может иметь целый ряд особых облаете!! (см. § 16.1), то может возникнуть потребность в отдельном определении области неустойчивости путем использования нижеследующей теоре.мы Ляпунова, которая дает достаточные условия неустойчивости системы.

Теоре.ма формулируется так: если при заданных в форме (17.45) уравнениях системы п-го порядка производная W (Xj, л 2,..., х ) от какой-нибудь функции Ляпунова V{x, Х2,..; х ) окажется зпакоопределенной, причем сама функция V в какой-нибудь области, примыкающей к началу координат, будет иметь знак, одинаковый со знаком производной W, то данная система неустойчива.

Справед.;гивостьэтой теоре.мы иллюстрируется геометрическиследуюпигм образо.м. I lycTb для какой-н ибудь заданной системы второго порядка (и = 2) найдена такая :п1акопере.менная функция F(Xj,X2), для которой производная

/ ВозмушЛ 1возлейст.7

(самолет)

ч.:-).1 \и.

Свободный

фу Свободный

Упранляи- У гироскоп Ч g мыиоГллкт =

X Скоростной f гироскоп --

Управляющий орган (руль)

Элсктро-дви1-атель с редуктором

P8-FW

Жесткая 1- обратная свм:*ь

Рис. 17.12

НОМ виде) был рассмотрен в работе А. И. Лурье и В. Н. Постникова. Схема данной системы представлена на рис. 17.12, я.

Пусть все звенья системы являются линейны.ми, за исключением электродвигателя (с редуктором), для которого будем рассматривать его реальную характеристику (рис. 17.12, б). Она может иметь произвольное криволиггейное очерташю с зоной застоя (при I (/1 < А) и с зоной насыщения (нри \U\> 2)- Наклон характеристики и ее криволинейность могут быт ;1юбы.ми, лищь бы только соблюдались условия

>0, F>0 при f;>A, и f<0 при U<-by

(17.54)

Требуется найти условия устойчивости данной системы.

Уравнение са.молета как управляемого объекта в грубо упронтенном виде будет

(Г,р-И)р\/ = -,6,

где 1/ - отклонение курсового угла самолета; 5 - отклонение руля.

Уравнения чувствительных элементов (гироскопов с потенциометрами):

(/,= k2\\l, U2=kp\\l.

Уравнение обратной связи Уравнение усилителя

Уравнение электродвигателя с редуктором и руле.м

(17.55)

(17.56) (17.57) (17.58)

где F(U) задается графиком рис. 17.12, б.

Для перехода к уравнениям вида (17.45) введе.м новые переменные:

1 Is Is X, =-Г-РЦ1+-о. --о.

1 1 /< с

Хз =-и = ----Ц1 +-рц1----о

(17.61)

и безразмерное вре.мя

(17.62)

С введением этих пере.менных дифференциальные уравнения всей системы (17.55), (17.59), (17.60) преобразуются к виду (17.45), а именно:

= -Х, +/(Хз),

dx2 It

= -/(з).

= (у-1)х,+ух2-г/(хз).

(17.63)

k к к f{x,) = F{TMpx,l

(17.64)

т. е. функция/(хз) имеет все те же свойства, что и .заданная функция f (f/) (рис. 17.12, б), и отличается лишь маспггабом чертежа но оси абсцисс в связи с заменой переменной U на Хз согласно третьему из равенств (17.61).

Установившийся процесс полета при данной системе согласно (17.55), 07-59), (17.60) и графику рис. 17.12, б будет и.меть место при

5 = 0, р\\1 = 0, \/

pv

(17.65)

Уравнения (17.56), (17.57), и (17.58) .можно свести к одному:

и = кЦ! + kj,pwf - Ai ,5, (17.60)