Тогда уравнение (3.5) примет вид

7з*Д.г-з + ГгАз + Г,Дгз + Ах- - кАх + к-Ах. + к-Ах2 + k/J(t).

(3.9)

В случае, если нелинейная функция Fne содержит величиныз, а содержит только ее производные, т. е. если

= 0,

дх-:

в формулах (3.8) необходимо заменить нсние

ГгДдгз +T Ах + Алгз =кАх + к2Ах2 + кАх2 + k/J(t),

. В результате получится урав-

(3.10)

дх-.

(dF]

:i J

Эхз j

Уравнения (3.9) и (3.10) удобнее записывать в символической форме, введя ал-гебраизировапиый оператор дифференцирования р = d/dt . Тогда уравнение (3.9) примет вид

{TIp + Tjp- +Тур + 1)Агз = , Дл-, + (/ + к-р)Ах2 + kj (t),

(3.11)

а уравнение (3.10)

iTip+l\p + l)pAx =,Дг-, +(к2+к.,р)Ах2+кМ).

(3.12)

Эти записи надо рассматривать только как сокрап1енпую форму более полных записей (3.9) и (3.10).

Стандартные фор.мы записи уравнений звеньев автоматических систе.м (3.9) и (3.10) или их сокращенные виды (3.11) и (3.12) можно использовать как для размерных отклонений реальных величин на входе и выходе звена, так и для любых безразмерных относительных отклонений, специально иногда вводи.мых для упрощения вида уравнений и удобства их исследования. При записи уравнений в стандартной форме коэффицие1ггы k, 4 пазьщаются коэффициентами передачи, а Т Тз, Гз - постоянными времени данного звена.

В случае звеньев, у которых выходная и входная величины имеют одинаковую размерность, для коэффициентов передачи используются также следующие термины:

1) коэффициент усиления - для звена, представ.;1ЯЮП1его собой усилитель wn\ имеющего в своем составе усилитель;

2) передаточное число - для редукторов, делителей папряжепия, масштабирующих устройств и т. д.

в) Дхз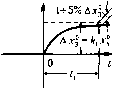

Рис. 3.3

Термин коэффициент передачи можно пояснить следующим образом. Если подать на вход звена только постоянное значение Дг (рис. 3.3, б) и найти установившееся значение выходной величи1П>1 Ах\ (рис. 3.3, в), то из (3.9) получим Дгз =kAx. Таким образом, коэффициент показывает отношение выходной величины звена к входной в установившемся режиме.

Следовательно, коэффициент передачи определяет собой наклон (с учетом масштабов но осям) линейной статической характеристики звена (рис. 3.3, а). За.метим, что нелинейную характеристику звена часто называют характеристикой с переменной но входной величине коэ4:>фициентом передачи. Из (3.9) очевидно, что

размерность =

размерность выходной величины Агз размерность входной величины Аг,

В размерность коэффициента передачи .может входить также время L. Так, из уравнения (3.9) следует, что

раз.мерпость Дз х раз.мерносП) t

размерность =-~---,

размерность Дг2

а из уравнения (3.10) следует, что для такого звена

размерность ДУз

раз.мерпость =

размерность ДГ] х раз.мерпость t

. ДГ] X раз.мерпость t.

Постоянные времени Г Т2 и /3, как следует из уравнений (3.9) и (3.10), имеют размерность вре.мени.

Вторая форма записи. Считая условно оператор дифферепцирования р = d/dt алгебраической величиной, решим уравнение (3.11) относительно выходной величины:

Дгз(0--

,Дг,(0

(2+зР)2(0

Выражения

(3.13)

Щр) =

W2ip) = Wf(p)=

UT,p + Tip+Tip

l+7,p + 72V+7V

l + T,p + Tip+T.fp

гз 3

(3.14) (3.15) (3.16)

называются в теории автомагического управления передаточными функциями. Уравнение (3.13) можно представить в виде

Дгз(0 = W,{p) Ar,(0 + W2(p) дг2(0 + Хр)/,(0. (3.17)

Выражения (3.13) и (3.17) представляют собой символическую запись дифференциального уравнения (3.9).

Передаточные функции, формулы для которых устанавливаются выражениями (3.14)-(3.16), вводятся для сокращения .записи дифференциальных уравиепий и также представляют собой символическую запись дифференциальных уравнений.

Более строго передаточная функция определяется через изображения Лапласа (см. главу 7). Если ввести изображения по Лапласу входных и выходных величин звена:

АХ, (s) = 1[Дх, (01; AX2(s) = i[Ax-2(0J; AX3(.v) = i[M-3(01; f, (.0 = (Ol

где s = с -г;(о - комплексная величина, то передаточную функцию (3.14) можно строго определить как OTHOuienne изображений выходной и входной величин звена:

.(,. АХз(5) , к,

AX,(s) UT,s + ns+Ts

при нулевых начальных условиях и равных нулю остальных во.здействиях на звено; АХ2 i) = О и F, (s) = О . Аналогичным образо.м можно определить передаточные фу1С-кции (3.1.5) и (3.16). Поэтому вместо дифференциального уравнения (3.17), куда входят функции времени Ax{t), Ax2{t) , Ax-(t) и/,(г) можно написать при пулевых начальных условиях уравнение для изображений в виде, совпадающем по форме с (3.17):

АХз(5) = Wi(s) АХ,(.0 + W2(s) АХ2(.0 + Wj{s) / ((s), (3.19)

или в развернутом виде:

А;з(.) = (> + (k2ks)AX2is) Wf)

В двух последних выражениях фигурируют не функции времени, а их изображения: АЛ,(.9), AX2(s), АХз(,) и F,(s), где s = с -Ь;(о - комплексная величина.

В изображениях Лапласа комплексная величина часто обозначается той же буквой р, что и оператор дифференцирования, причем р = с+]ш .В этом случае уравнение (3.19) будет иметь вид

AXip) = W,ip) АХ,(р) + W2(p) АХ2(р) + Wjip) F,(p). (3,21)

Здесь, как и в уравнении (3.19), фигурируют изображения функций АХ,(р),

В дальнейшем будет употребляться символ дифференцирования р = d/cit для символической записи дифференциальных уравнений, куда входят функции времени Ax(t), Ax2{t) и т. д., ко.мплексная величина р = с + j(o для записи уравнений с и;юбражениями функций времени по Лапласу АХ,(р), АХ2(р) и т. д. Запись передаточных функций звена и в том и в другом случае совпадают: Wip), UjCp) и т. д. Однако в передаточных функциях буквабудет означать символ дифференцирова1П1Я