Амплитуда первой i-армопики для треугольного сигнала с ограничением имеет вид

(18.161)

Ah . а.) --зшф. щ

Следовательно, первая гармоника сигнала 2 будет

. . Ah . . АЬ . 2 Х2 =а2 51п(Сог:~ф)= - зп1фсо.чф51па)г:--sin фСОВСО

Лф 71ф

(18.162)

в результате можно записать уравнение нелинейного блока (рис. 18.33) в, гармонически линеаризованном виде:

(18.163)

q = -

8Й --f

па ш.,

(18.164)

Характеристическое уравнение всей замкнутой системы при этом получит вид

k2Cyq + {kyCy+k2C2)

(jC] + k2C2)q + kiC2- p + kiC2q = 0. (18.165)

Для удобства дальнейших преобразований представим и - в виде

Ч ~ < ~ а Лд а

(18.166)

где Qi и 0 2 зависят от частоты со, а от амплитуды а пе зависят. Будем искать частоту сОп и амплитуду а автоколебаний путем подстановкир =jco (18.165), что дает:

Х = 2

21 - - (jC) + 22 ) -

со2=0;

(18.167)

(,С,+2С2)--lC2

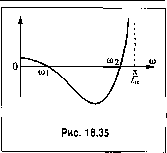(С, + k>C2 ) Q, - kiCQi -( - 2qQ2) = О-

(18.170)

Отсюда, подставляя значения полученных при решении уравнения (18.169) частот, можно найти амплитуду периодического решения а сигнала на входе нелинейного звена. Остается определить, которое из двух пайденюях решений соответствует дей-ствительны.м автоколебаниям в системе. Для ;этого исследуем устойчивость найденного решения с помощью критерия (18.63).

Поскольку согласно (18.167)

частная производная

{да)

X = -F,(4i), а

так каквыраженис, (ю) представляет собой левую часть уравнения (18.169), обращающуюся в нуль при ш = ш .

Для отыскания представим У в виде

Тогда

¥=-Р2(а,ш). а

--i-2(a,(o)+-- а да

<0,

так как выражение F2 (а, со) представляет собой левую часть уравнения (18.170), обра-цающуюся в нуль при ш = со , а = а ,а частная производная

Поскольку я 5* О, из (18.167) можно иайти частоту со :

kc2Qi -IViai -(V2 +2)<2гН =0. (18.169)

Так как в Q] и Q2 входит со под знако.м тригоно.мет-рических функций, решаем это уравнение графически. Его левая часть изображается кривой, показанной на рис. 18.35.

В результате получаются двазначения частоты периодического решения: со = со, и со = щ.

Преобра,зуе.м уравнение (18.168) к виду

В результате условие устойчивости колебаний (18.63) сводится к требованию

>0. (18.171)

При отыскании частоты со автоколебаний по уравпе1П1Ю (18.169) был построен график f, (0)) аХ (а, со). Из рассмотрения этой кривой (рис. 18.35) видно, что условие устойчивости (18.171) выполняется для большего из найденных зиачеиий частоты со = СО2. Таким образом, в систе.ме существуют автоколебания, параметры которых определяются указанными зршчениями частоты со = СО2.

Помимо условия (18.171) для устойчивости найдеппого peniemw неоГ>ходимо, чтобы все коэффициенты характеристического уравнения (18,165) были положительными, а именпо;

/ / /

l + k2Cy - >0, [kyq+k2C2)q + kiC2~>Q, k2Ciq + [kiCi+k2C2)->0, Ay;2>0.

Легко проверить, что все эти условия были вьнюлисны в само.м процессе отыскания нерис)Дического решения.

§ 18.5. Вычисление высших гармоник

и уточнение первой гармоники автоколебаний

Пусть .задано дифс]1еренциачьное уравнение нелинейной системы

Q(p)x + R(j))Fix,px) = 0. (18.172)

До сих пор периодическое решепие (автоко.тебаиия) для иелииейиой сис темы искалось для первого приближегшя в виде

.r = asinco£, (18.173)

что соответствовало приближенному значению первой гармоники периодического решения. Все высише гармоники при это.м отбрасывались ввиду их матости при наличии в системе свойства с{)ильтра (§18.2).

Оставляя в силе это условие, произведем отыскание малых выситих гар,мопик [72], введя отдельное обозначение для каждой k-и гармоники:

Xk ? ,asmikb}it + ) (J 2, 3,...), (18.174)

где амплитуда -й гармоники 5а выражена через а.мплитуду первой гармоники а, причем коэффипиент 5 является малой величиной (так как амплитуда высшей гарм01Ш-ки предполагается .мшюй по сравнению с амплитудой первой гармоники). Величину 5, играющую в даппой задаче роль матого параметра, можно назвать отпосите.тьной амплитудой k-й гар.моники.

Теперь с учетом конечного числа п выснигх гармоник искомое периодическое решение запишется в виде

х = ,г,+Х-г*, (18.175)