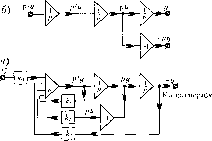порядок дифференциального уравнения, которое может быть исследовано иа данной модели. Кроме того, имеется ряд вспомогательных усилителей, при noMonui которых можно осуществлять онеращти умножения на постоянный множитель (масштабирование), перемены знака (инвертирование) и суммирования.

Исследуемые процессы в виде из.менения .машинных переменных (напряжений) могут наблюдаться и фиксироваться при помощи ос1щллографов и фа<[)ОПостроителей.

Для приложения к элскгрогнюй модели исследуемой системы задающих и воз.мущающих воздействт ! исполь.зуются геие[)ато-ры, которые .могут воспроизводить требуе-.мыс фуикпии времени, например линейную функцию, синусоиду, экспоненту, пря.моу-гольную или треугольную волну и т. п., в виде соответствующего изменения электрического напряжения. Существуют также генераторы случайных величтг

Кро.ме того, электронная модель имеет ряд вспо.могательных устройств, позволяющих после набора исследуемой задачи производить пуск и остановку решения дифференциальных уравнений, фиксацию решения в заданной точке, периодизацию решения и т. п.

Набор задачи на электронной моде;ш структурного тина может быть осуществлен двумя способами;

1) по /шс1)<1:)еренциальному уравнению, которы.м описывается исследуемая система;

2) по структурной схеме исследуемой системы.

Рассмотрим порЯдок набора задачи на простейшем примере. Начнем с первого способа. Пусть дана система, структурная схе.ма которой представлена на рис. 7.6, а. Для .этой схемы передаточная функция разомкнутой системы

Рис. 7.6

Щр)=-.

(7.-53)

\ + 1\р pi + rp)

Диффе15епциалы1ое уравнение ; мкпутой системы, записанное в символической форме, в соответствии с гл. 5 будет

[1+ w(p)\y(t)- \V(p)g(t),

где г/(/.) - управляемая величина ag(0 - ;!адающее воздействие. В рассматриваемом случае, учитывая (7.53), получи.м

(ар + щр + a.jp + з) yit) = ag{t). (7.54)

о = F{1\; а, - 1\ + Т/, a.f-\ и а.з =

Перейдем к маплшиым переменным Y = т,у и G = 1Г.£. Учитывая сос)тноц1ения т = тС и = тР , получим из (7.54) дифферетцпктьпое уравнение для мапгиппых переменных:

(ЛоР + А,1 + АР + А,) Y(x) ~- B,G(x),

(7.55)

где .% = mfoo, Ai = тщ, А = mfl Л3

Уравнение (7.55) разрешим относительно старшей производной:

РуЛс-рЦ-

(7.56)

4 Л А)

рассмотри.м цепочку из трех последовательно включе1нн>1Х интеграторов (рис. 7.6, б). Если ГШ вход первого интегратора поступает величина PY, то па его выходе получится, сучетом 1геремены знака, величина - FY, па выходе BTopoio шггеграто-ра - величина РК и на выходе третьего интегратора - величина - К В результате можно реализовать дифференциал)>ное уравнение (7,56), если на входе первого интегратора сложить с учетолг знаков и маспггабов все члены, входяпше в правую часть формулы (7.56). Это цоказа1и) на рис. 7.6. в. 31шчения коэффштеитов делителей

k -Ik k - А 4 Ai определяются выражениями ю - , > М -~Г 2 ~Т~ н ~~Г

/1о Л(, Aq /1у

Задавая теперь управляющее воздействие G(x) от генератора (})ункций времени и вводя начальные значения, можно исследовать поведение маши1И10Й переменной К(т), которая отображает поведение управляемой величины y(t) в реа;ияюй системе.

Второй способ набора задачи пазлектрониой .модели ;!а1слючается в TONr, что восп[)о-изводится структурная схема, изображенная на рис, 7.6, а. Звено второго порядка удобнее щюдставить в виде последоватечыго вюиочеипых звеньев первого порядка, каждое из которых .может быть реа.!П1;ювано на ба,)е одного интегратора. Это представлено на рис, 7.7, а. Схема набора, пос.трое1Н1ая в соответствии с табл. 7.3, изоб{)ажена i la {жс. 7.7, б.

Для уяс11еггия методики подсчета коэффициентов расемотрн.м, например, второе звено (рис. 7.7), Исходная передаточная функция имеет вид

Л2(р),

(7.57)

х,(р) 1 + Г2Р Для маппгиных пере.мепныхХ, = тх, и

2- 2 уравнение запишется в виде

Х[ т, i + T2miP От(Ж)да находим

(7.58)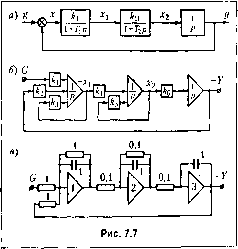

Это уравнение и набрано на втором интеграторе (рис. 7.7, б). Передаточные коэффициенты усилителя по соответствующи.м входам определяются из (7.59):

(7.60)

(7.61)

Аналогичным образом составляется схе.ма набора остальных звеньев, входяп1Их в структурную схе.му (рис. 1.1;а).

Получившаяся схема набора (рис. 7.7, б) представляет собой совокупность операционных усилителей в режиме интегрирования, за.мкнутых местными отрицательными обратны.ми связями.

Другой метод структурного моделирования заключается в том, что элементы структурной схемы представляются в виде типовых звеньев, набираемых па операционных усилителях в соответствии с табл. 7.3. На рис. 7.7, в изображена подобная схема набора для случая, когда , = 1, = 10 с . Г, = 1 с и Г2 = 0,1 с. При наборе принят натуральный .масштаб времени ( т, = 1 и t = x).

По сравнению с .моделированием дифференциального уравнения (рис. 7.6) моделирование структурной схе.мы и.меет преимущество в смысле большего соответствия модели исследуемой систе.ме. Кроме того, моделирование структурной схе.мы позволяет просто учитывать при исследовании системы типичные нелинейности, например ограничение переменной величины, зону нечувствительности, релейную характеристику, люфт и т. и. Эти характеристики могут быть реализованы в электронной

модели посредством исиоль-;ювания диодных элементов. В табл. 7.4 приведены некоторые типичные пе.чинейности и электрон1Н)1е схе.мы с диод-ны.ми элементами, позволяющие реализовать в .модели эти характеристики. Кро.ме этих простеЙ1ПИХ пелинейных блоков в электронных .моделях применяются более сложные схемы, позволяюппге реа.ли;ю-вать различные криволинейные характеристики, операции возведения в степень н извлечения корня, операции перемножеггия двух переменных и т. п.

На рис. 7.8 для иллюстрации приведена структурная

g 0-