а иа первого

Формула (18.70) дает график, изображенный па рис. 18.13, й, где

Рис. 18.13

О Юнаим (Оп (О

со =

(18.72)

Графики па рис. 18.13, б и определяют связь между амплитудой а и частотой периодического решения в данной системе.

Найдем зависимостьамп.чигуды а от величиггы параметра к. Для .этого, .задаваясь ра.зличпы.\н1 ю будем брать из графика рис. 18.13 соответствуюпдие 31шчепия а , а по формуле (18.71) вычислять к. В рс-.зультатс получим график а {к) типа рис. 18.14, а или б. Чтобы определить, в каких случаях каждый из них имеет .место, Егайдем , 1 . Дифференцируя (18.71) по ю с учето.м (18.70) и приравнивая результат нулю, нолучае.м соответствуюпхее значение со, в виде

(18.73)

причем/;,nj оггределяется нодстаиовкойсо в (18.70) и (18.71), а и.менно;

(18.74)

Очевидно, что если ю, > ю , то ire существует и имеет место первый случай (рис. 18.14, а), а при со , < сОд ~ второй (рис. 18.14, б). Сравнивая (18.73) и (18.72), приходим к выводу, что для системы, параметры которой удовлетворяют условию

(18.75)

справедлив график на рис. 18.14, а, а для системы с параметрами

1 +

- на рис. 18.14,(9.

Исследуем устойчивость найдетюго периодического решения по критерию (18.63). Согласно (18.66) частота а не входит в ко.эффициегггьг 11оэ1 ому в выражении (18.45) для кривой Михайлова функции Л(м) и У (м) совпа,цак)тс (18.69).

Найде.м ггроизводные:

-2\Т +Т, +Т,кд(а )]ш =-2r ra (l + 7;>f,)<0,

(дХ\

[да J

= 1 + kci(a ) - 37;Г ш2 = -2TJ,bii < О, (dq] (T +T,)ixi(dq]

<7(a )

<0,

У da ,

<0,

(18.77)

так как соглас11о рис. 18.13, б производная dq/da отрицательна.

Легко проверить, что при сй> со, где со оггределяется формулой (18,73), критерий (18.63) удовлетворяется, а П1)и сй< со, не удовлетворяется. Отсюда делаем заключение, что все периодические решения па рис. 18.14, а устойчивы (т. е, соответствуют автоколебаниям). Вертикальными стрелка.ми та.м показано, что переходггые процессы сболь-гггими и .меггьши.ми акпыитудами сходятся к даггному ггериодическо.му П1)оцессу. На рис. 18.14, б только верхняя ветвь кривой (выпге точки ю ) соответствует устойчивым периодически.м регнепиям, т. е. автоколебаниям, а нижняя (со, + to ) - неустойчивым.

Как уже отмечалось, через а здесь обозначена а.\гплитуда колебаний величины Чтобы узнать амплитуду Яр автоколебаний уггравляе.мой величины Р, надо воспо;гь.зо-ваться уравнением (18.65), откуда

С1(а ) 7;,Г,.сй?, -1

а =

(18.78)

как модуль соответствующей ггередаточной функции при р =;ю, умножениый на а . При это.м величины а и ю определяются графиком рис. 18.14, я или б.

Учитывая, что (я) ky при я =6 (см. рис. 18.13, б), найдем гю формуле (18.71) с подстаповкой = сй, из (18.72) величину k, от.мечепную гга рис. 18.14;

г +7:

(18.79)

Точно такое же значение является граниг1ей устойчивости для линеГпюй системы, когда уравнение управляе.мого объекта с двигателем вместо (18.65) имеет линейный вид (TiP + 1) рР = kyi. Отсюда можно сделать вывод о том, что в счучае (18.75), для которого имеет место график рис 18.14, я, данная нелинейная система сохраняет устойчивость в той же области, что и линейная система, но она обладает сиге установив iuhmch автоколебательным режи.мо.м та.м, где лшгейная систе.ма неустойчива. Сле-

Рис. 18.15

довательно, ограничение линейной характеристики тина насыщения в двигателе (рис. 18.13, в) препятствует раскачиванию системы, которое получается при > в линейной системе. Это наблюдается и па практике.

В случае же (18.76), для которого график, определяюп1ИЙ автоколебания, и.меет вид рис. 18.14, б, автоколебания могут уже появиться ггри k > й (но > /г,), т. е. раньше наступления границы устойчивости линейной системы. Но в ;)то.м случае, как видно из рис. 18.14, б, при малых началыплх а.мплитудах иереходпого процесса (ниже кривой ю,(Од) сохраняется ente устойчивость равновесного состояния. Здесь в области параметров й <k< к (рис. 18.14, б) и.меется как бы два предельных цикла (рис. 16.14, в), а в области к< k<°° - один.

Случай, изображенный на рис. 18.14, б, называется жестким возбуждением автоколебаний. Такое возбуждение автоколебаний раньпге ггаступления границы устойчивости В03.М0Ж1Г0, как видно из (18.76), только ири достаточно больпго.м kg, который, ио cyniecTBy, является коз(}фици.енто.м гибкой обратной связи. При отсутствии такой связи указанное явление не имело бы .места.

На рис. 18.15, а и б даны графики для величины частоты автоколебаний со в зависимости от 1гара.метра соответственно для случаев, изображенных на рис. 18.14, а и б.

П р и м е р 2. Рассмотрим теперь следящую систему с линейной характеристикой привода, но учте.м сухое трение совместно с линейны.м (рис. 18.16, а). Уравнеиие управляемого объекта с двигателем имеет при это.м вид (16.52). Здесь возможны два случая: 1) колебания без остановок, когда обеспечиваются усювия первого из уравнений (16.52); 2) колебания с остановка.ми, когда действуют понереметю оба уравнения (16.52). Рассмотрим первый случай и определим условия его существования. Итак, записываем первое из уравпеггий (16.52), поделив его ira С2 в виде

7;,р2р + p + kj signрр = ki , = -

к,Х Т. и.

(18.80)

с условием,что

я >у при рР = 0, (18.81)

Обозначим X = pp. Тогда это уравнение будет

а]р т i)x + F(x)=k,i, (18.82)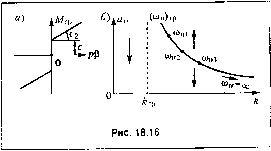