еГ ТТ+еТ 2Т2Т+еГ I О

Рис. 14.5

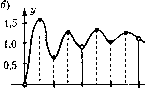0,5Г Т Г+0,5Г 2Т t

Решение ра.зностного уравнения y{i) дает .значения выходной величины лишь в дискретные моменты времени t = iT. Во многих случаях этого вполне достаточно для суждения о поведении системы. Если же возникает необходимость в получении информации об изменении выходной величиш>1 в любой момент времени, то используется смещенная последовательность (рис. 14.5, а)

г/(гТ + еГ) = г/(0,-,т.Е7-.

(14.15)

или в сокращенной записи y{i, е), где е - параметр, которому можно придавать любые значения в пределах О < £ < 1. Если е изменять непрерывно в указанных пределах, то г/(г, е) совпадает с y{t).

Смещенная последовательность г/(г, е) представляет собой решение разностного уравнения со смещенньш аргументом

CQy(i + п,г) + с, y(i + п - \ ,е) +...+ c y(i + 8) = Ь(г) u{i +т) + + /;,(£) u(i+m- 1) + ...+ й, (е) u(i),

(14.16)

которое при е = О превращается в уравнение (14.10).

Значения выходной величины y(i, е) .можно вычислить последовательно шаг за шагом при заданных начальных значениях и значениях входной величины u(i).

Переходная составляющая, т. е. обнсее решение однородного уравнения, определяется в этом случае следуюш;им образом:

у(г,г) = СУ + С22+...+ СГ (14.17)

где2,(у =1,2, ...,п) - некратные корни характеристического уравнения (14.1.S).

В качестве примера исследуе.м процессы в системе, разностное уравнение со сме-П1енпым аргументом которой и.меет вид

y(i + 2, е) - 0,27г/(г + 1, е) + 0,135z/(f, е) =

== (1 - е- cos 4пе ) u(i +2) - (0,135 - е cos 4п£ ) u(i +1)

(14.18)

при начальных значениях г/(-1, г) = у{- 2, е) = О и единичной входной последовательности м(0) = м(1) = ... = 1.

Положив е = О, получим обыкновенное разностное уравнеиие:

y(i + 2)-0,27y(i+ I)+ 0,1.35.2/(0 = 0,865 м(г+ 1). (14.19)

Корни характеристического уравнения

z2-0,272 + 0,135 = 0;

2i,2-0,135 ±;0,34

удовлетворяют условию (14.14). Следовательно, система устойчива.

Из (14.19) приу(-1) =у(-2) = О последовательно шаг,за шагом находим значения выходной величины в моменты времени с = гТ:

у(0) = 0,27.v(-l) - 0,1,35 г/(-2) + 0,865 м(-1) = 0; у(\) = 0,27 у(0) - 0,135.г/(-1) + 0,865 м(0) = 0,865;

у(2) = 0,27 .( 1) - 0,135 .(0) + 0,865 м( 1) 1,098; .(3) = 0,27 у(2) - 0,135 г/(1) + 0,865 м(2) = 1,045,...

Продолжая вычисления, убеждаемся, что в дискретные .мо.менты времени i = iT процесс монотонный, а выходная ветчина стремится к установившемуся значению у =1.

Аналогично решая уравнение(14.18) получи.м:

.V(0, £) = 1 - е cos Апе ; /у(1,е)- 1,135-0,27р Чч)з4пе; у(2, е) - 1,036 + 0.062 е cos Апе,...

Кривая г/(0 изображена на рнс. 14.5, б, где отмечены ее значения при е = 0; 0,25; 0,5; 0,75. Таким образом, реальный процесс в систе.ме колебательный ;!а1ухаюн1;ий, что не обнаруживается в результате решения уравнения (14.19).

Способы получения разностных уравнений будут рассмотре1п>1 в следующих параграфах.

§ 14.3, Использование z-преобразования

Для последовательностей /(г) может быть введено понятие дискретного преобразования Лапласа, определяемое формулой

F4p) = lf{i)c- (14.20)

Для смещешгых последовательностей может быть записано аналогичное выраже-

ние:

/*(Р,) = Ё/(е)е- . (14.21)

Формулы (14.20) и (14.21) можно представить в символической записи:

P(p) = D(/(f)}, (14.22)

е) - у;, {/(;, е)}. (14.23)

В приведенных формулах, как и в случае пенрерывного П1)ео5разован11я Лапласа, комплексная величина р = с + jay, где с - абспшч:а абсолютной сходи.мости. Нс.ми с < °о, то ряд, определяемый формулами (14.20) и (14.21), сходится и оригиналу/(г) соответствует некоторое изображение.

Как следует из (14.20) и (14.21), и.юбражение является функпией величины е

Для исследования импульсных систем болыиое распространение получило так иазьп5аемое2-преобразовапие, которое связано с дискретным преобразованием Лапласа и вытекает из пего. Применительно к г-иреобразовапию ниже будут рассмотрены ооювные свойства и теоре.мы дискретного преобразования Лапласа.

Под z-преобразованием пони.мастся изображение иесмстеииой или смспнчпюй последовательностей, определяемое формула.м и

/ Хг) = £/(/> , F(2,e) = ffm)z. П4.24)

/-0 ;=()

В этих формулах введено повое обозпачениег = еИз них cJicviyer, чтог-нрсобра-зовапие практически совпадает с дискрет)пям п[)еобразова1П1е.м Лан;1аса и отличается только а1)гу.ментом изображения.

Формулы преобразования (14.24) могут быть записаны в символической форме;

Fiz)-Zmi F{z,z) = Z,{f{i,z% (14.2,5)

Формулы преобра;ювания (14.25) могут быть записаны и для иепрерывпой нронз-водянтей функции в виде

f(z) = Z(/(0}, t-iT,

F(z,i:)-Z,m\, t = ii + )T, -

где i =0, 1,2,...

Ряды (14.24) сходятся, и изображение суптествует, если выполняется условие, сформулированное выше для дискретного преобразования Лапласа; с < оо, где с - абсцисса абсолютной сходимости.

В табл. 14.1 приведены изображения некоторых последовательностей, а также про-изводянщх фущсции времени и их изображений Лапласа.

Для всех иепрерыкиых функций и последовательностей, приведе1ПИ)1Х в табл. 14.1. пред1юлагается, что они тождественно равны нулю при f < 0. В некоторых изображениях табл. 14.1 использованы полиномы Riz), которые могут быть представлены в виде определителя [ 96 ]

Ru=k\

1 1-2

2?

1-2 1

... О ... О

... О

k\ (й-1)! {k-2)\

(14.27)