Расчет по формулам первого приближения (18.126) и (18.128) дает автоколебания в виде X = а sin ю, где для варианта слабо11 пелипейности

а=8,14, ю = 6с ,

а для варианта сильной нелинейности

а = 0,834, ш = 6с-.

Вычислим теперь высшие гар.моники. Для учета второй и третьей гармоник воспользуемся формулой (18.178). Для рассматриваемой в настоящем примере нелинейности F{x,px) ко.зффициенты и s подсчитанные по формулам (18.177), оказываются нулями. Поэто.му остается только третья гармоника, для которой по формуда.м (18.177) для данной нелинейности с учетом обозначений (18.121) находим:

5 .3 э

Тогда по фор.мула.м (18.179) с учетом того, что согласно (18.124) QО) = (7> + 1) (Т,р + \)р + kA R(p) = {Т,р + \)р, находим относительную а.чшлитуду и фазу третьей гармоники:

(18.204)

5з = Зсо

2 , 2ч

/г, - 9( Г, -(- 7з )юЧ% 9ю2 (1 - 9Т, Гз)

Фз = - -f-arctg3r,ra-aretg----ь arctg

При указанных вып1едаг[ных получаем для варианта слабой нелинейности

а Для сильной нелинейности

5з = 0,041, фз =-0,377,

5з = 0,042, фз = -0,384.

После этого уточняется первая гармоника автоколебаний а, sin cOjt Для этого по форму.та.м (18.183) находим величины добавок hq и Aq к коэффициентам гармонической линеаризации:

3 (2 Л

Aq-Tbyаа)5зsiпфз - - 2 + за а5зcosфз;

э \jj

2 (3

Aq= -Гзй,аа)5з созфз - -Ь2+Ьа a5зsinфз.

5 \э J

Поэтому новое характеристическое уравнение для определения уточненной первой гармоники будет

(rjP + \) + (TJbap + h2a+bra) {Тр + \)р+ kk+ Aq+--p {Тр + \)р = 0.

Подставляя р = jco, и выделяя вещественную и мнимую части, получим

7з(1+6а,)-нГ,(1+б2а, +ha1)

ю, -

Ihq +-р

,3 Г Д?,.,3

cof =0;

Эти уравнения решаются тем же методом, что и (18.125), а именно: из второго уравнения получаем

2 1 + 21 +b-ia +Aq

а из первого.

k= Тз(1 + 7,а,)-1-Г,(1-1-?2а, н-за)-!- TAq +

со?.

Эти уравнения приводят также к графику а, (к) вида рис. 18.23, в. Для приведеупых выше числовых значений параметров системы получаем следующие уточненные значения амплитуды и частоты автоколебаний:

- для слабой нелинейпости

а, =8,03, ю, = 5,99с,

- для сильной нелинейности

а, = 0,820, 0), = 5,98 с .

Как видим, сильная нелинейность значительно снижает амплитуду автоколебаний (в линейной систе.ме было бы а, = °°). Этот результат получался выше в pcnjennn по первому приближению и подтверждается теперь уточненным репюпием.

Нелинейность в данном при.мере характеризует степень отклонения реальной криволинейной характеристики двухфазного индукционного двигателя от прямолинейной.

§ 18.6. Частотный метод определения автоколебаний

Здесь, следуя Л, С. Гольдфарбу [89], будем рассматривать простые иелипейпости Х2 = так как в других случаях (юлучаются более сложные графические пост[)ое-

ния.

Пусть в нелинейной системе выделено, как обычно, нелинейное звено. Разомкнем систему указанным нарис. 18.38, я образо.м, причем уравнение нелинейного звена будет

X2 = F(.r,), (18.205)

а линеЙ1[ои части системы -

Q{p)x., = R<j>)x2.

(18.206)

Замыкание системы соответствует замене

лз= -X,. (18.207)

Подади.\1 на вход нелинейного звена (рис. 18.38, а) синусоидальные колебания

Xi=as\\\iMt. (18.208)

На выходе пелипейпого звена получи.м согласно (18.205) вынужде1П1ые колебания

X2 = f(asincoO, (18.209)

которые можно найти, например, как показано нарис. 18.38, били в. .

Раз.южим (18,209) в ряд Фурье и сохраним то;1ько основную синусоиду (первую гармонику, отбросив все высшие i-армоиикп. Очевидно, что это приближенное представление вынужденных колебаний эквивалентно гармонической линеаризации нелинейностей, рассмотренной в § 18.1. Наосновании этого для определения первой гармоники вынужденных колебаний величины Хз можно воспользоваться частотиы.м ainia-ратом, который нри.мспялся ранее для лиггейных систем следующим образо.м.

Согласно фор.мулам (18.9) приближенная передаточная функция нелипейногозвена

с уравнением Хз = f (х,) будет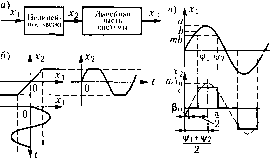

W =qia)

соответственно при наличии гистерезисной петли и при ее отсутствии. При этом выражения q (а) и q (а) определяются формулами (18.10).