Крайние точки особого отрезка CD определяются, очевидно, как точки, в которых прямая АВ касается одной из парабол соответственно правого и левого сехгейств, По-

этому, подставив значения из (17.7) в выражение (17.10), найдем точку С:

По найденной картине расположе1П1Я фазовых траекторий можно качестве1п ю представить себе кривую переходного процесса ф(г) при любых тгачальных условиях. Начальными условияхп! оггределяется начальное положение изображающей точки М и тем самым - определеипая фа;ювая траектория, иллюстрирующая п[ютекание процесса. Она показывает (рис. 17.1, а) максимальное отклоиенрге управляемой величины ф, ,д, максимальную скорость (рф) а также все последующие отклонения, число колебаний ИТ. п.

Рассмотрим теперь ту же систему, но с учетом зоны нечувствительности. В этом случае переключениям привода (при о== -Ь и а = +h) на фазовой плоскости соответствуют согласно (17.6) две наклонные прямые (рнс. 17.1, б):

X = -бГд у-Ьб и X = -57 у й5.

Между эти.ми пря.мыми \a\<h, правее их а < -h, левее nxa>h (причем b > 0). При \о\<Ь из (17.4), (17,6) и (17,5) получаем

du dx

--f = 0, -=г/,

dt dt

откуда (при i/?i0)

-0 или .г/=6з

(прямые, параллельные оси х в полосе па рис, 17,1, б).

При I а I > й пoлyчн прежние параболы. В результате снова систе.ма оказывается устойчивой и имеет колебательный переходный процесс, но вместо особой точки О по.тучаем особьпг от1)езок (у = О, -ЬЬ <х< ЬЬ), т. е. устаповивишеся состояние определяется неоднозначно. Это соответствует тому, что систе.ма .может находиться в равновесии в любом месте внутри зоны нечувствительности. Здесь точно так же воз.можен скользяищй ироцесс, как и в случае рис. 17.1, а.

В дашюм при.мере система оказывается устойчивой при любых значениях параметров и при любых иачатьиыхусловиях. Однако здесь для получения систе.мы второго порядка была проведена грубая идеализация уравнений (иренебрежепие массой й демпфированием).

Пример 2. Допустим, что требуется стабилизировать угловое положение некоторого тела, например космического аппарата, когда сопротивлением среды его вращению .можно пренебречь. Уравнение обьекта будет

J = M, со = . (17.11)

dt dt

где/ - момент инерции тела; ф - угол поворота тела; со - его угловая скорость; М - управляющий момент со стороны иснолиитсль-иого органа системы стабил изацин.

Уравнение управляющего устройства за-nnnicM в виде

М= М,Ф(ф, со),

(17,12)

Рис. 17.2

гдеМ, - постоянная положительная ве.тичи-на, Ф(ф, со) - нелинейный алгоритм управления, осуществляемый при помощи ло1 ичес-кого устройства по тому же нростейн1ему принципу, что и па рис. 16.26, с той лип1ь разницей, что по углу ф фазовая плоскость ограничена значениями -t-л и -л, так как это составляет о.тип полный оборот тела (рис, 17,2), Изобрази.м процесс управления иа фазовой плоскости. Уравнение всей системы согласно (17.11) и (17.12) будет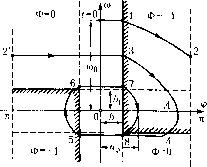

с/со ИГ

= СФ(ф, О)),

(17,1,3)

где обозначено

с = -

причем с имеет физический смысл величины углового ускореггия, сообпшемого данному телу постоянным .моменто.м М,.

Умножив почленно уравнение (17.13) на выражение

со =

сУф It

получим дифференциальное уравнение фазовой траектории

(О (/(О = с Ф(ф, со) dip.

(17.14)

Это уравнение легко интегрируется внутри участков, иа которых Ф = con.st, В результате для каждого отдельно взятого участка уравнение (})азовой траектории будет

ш ~ш1

=сФ(ф

Фн).

(17.1.5)

где ф и сОн - значения ф и со в начальной точке данного участка. Зададим начатьиыс условия процесса:

ф О, со = COq при I = 0.

Для данной нача.1ьн()й точки процесса (см. рис. 17.2) имее.м Ф 0. Поэтому па первом участке процесса согласно (17.15) уравнение фазовой траектория будет

со const = со,).

Этот участок движения с постоянной скоростыо закапчивается в точке 1 (рис. 17,2), где происходит вютючение исполнительного органа (Ф = -1). Следовательно, для второго участка процесса (после точки f) из (17,15) получим уравнение фазовой траектории

со - со, - 2г (ф - й), (17.16)

так как в начальной точке 1 этого участка ф = h, со = cOq.

Фазовая траектория (17.16) - парабола, ось которой совпадаете осью ф.

Это соответствует равноза.медленному движению . И.зображая параболу графически, доводим ее до границы ф = я (участок 7-2 на рис. 17.2), причем в точке 2 согласно(17.16)

= Jco;;-2c(7i-/;). (17.17)

Это значение пе])епоси.м в точку 2 (для вращаюП1егося тела ф = ±л - это одна и та же точка). Здесь происходит выключение исиолнительпого органа (Ф = 0). Поэтому дагьнейпюе движение согласно (17.15) пойдете постоянной скоростью

со = const = OJq

до точки 3 (рис. 17.2). Таким образом, в рассмотренной начальной части процесса управлепия тело совершило один полный оборот, но в Kontie этого оборота скорость вращения его стала меньше начальной.

В точке.? снова включается исполнительный орган (Ф = -1), в результате чего фазовая траектория будет

со2= 0) -2с(ф-й), (17.18)

гак как в точке 3 ф = h, со = СО2. Допустим, что соответствующая уравнению (17.18) парабола 3-4 не доходит до границы ф = л. Это означает, что тело больше не совершит полного оборота, а начнет (с точки Л) возвращаться в сторону пулевого [юложения.

В точке 4 (рис. 17.2) имеем скорость со, = -й,. Следовательно, из (17.18) угловая координата ее будет

г.те О), определяется по формуле (17.17).