Они получаются так же, как и уравпепия (23.51), если в решении (14.72) положить I = ГГ+еТ. Уравпепия (23.51) представляют собой частный случай (23.59) при е= 1.

Выражения для матриц (23.60), соответствующих типовы.м линейным непрерыв-пы.м частям системы, приведены в [57].

Уравнения (23.51), (23.57), (23.59) справедливы и для систем с lUHM-2 (рис. 23.11, а). В них только следует .заменить м пах = g-г/. Однако скважность и.мпульсов у, должна определяться из уравпепия (23.46), которое в общем случае является нелинейным.

Пример 1. Исследуемсисте.му с ШИМ-1 (рис. 23.10), передаточная функция линейной непрерывной части которой \¥{р) = к/р , camg{t) = Vt,D{z) = 1,/г = 15 с Г=0,1с,(3 = 1,У=5с-,г/(0) = 0.

В данном случае в уравнениях (23.48) А = А = 0, b = Ь = к, = с = 1, u = x = g-ij и уравнения (23.59) припи.мают вид

г/(г-(-е)= г/(г)-1-1,5е signx(/) при 0<е<у,-; г/(г-(-е)= г/(г)-1-1,5у/ signх(г) приу,<е<1.

Скважность импульсов согласпо (23.44)

Y/ =

x{i) 1

при x(/) < 1, при x(f) >\.

Ошибка системы

X {1 + г) = g{i + г)-у{1 + е) = 0,5 (г + е)-у{1 + г).

Решив полученные уравнения последовательно шаг за шаго.м, начиная с последнего, нолучим переходный процесс, изображенный иарис. 23.12.

. В моменты вре.мени t = гГ ошибка стремится к установившемуся значению Ху (г) = 0,33. Однако в промежутках между мо.мепта.ми замыкания устанавливаются незатухаюпие колебания или пульсации.

Пример 2. Исследуем систему с ШИМ-2 (рис. 23.11, а), если Wq{p) = к/р. g(0 = 1(0, 2= 10с ,Г=0,1с,(3= 1,.г/(0)=-0.

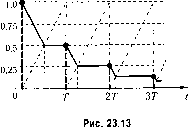Составляем уравнения системы:

- ошибка системы

x(i + e) = g(i + г)-y(i + e) = \-y(i + г),

- уравнения (23.59)

у(i + e) = у{0) + Е sign.r(f) нри0<е<у,-; z/(f + e) = z/(0) + Y,- sign .г (О приу,-<£<1;

- уравнение (23.46)

[l-.?/( + Y,)lsignx,.=Y,-.

Рен1ив эти уравнения последовательно шаг за шагом, начиная с последнего, получим переходный изображенный на рис. 23.13. Там же показан нилообразггый опорный сигнал. Установившаяся ошибка Xv = 0. Пульсации имеются только в переходном процессе.

Следует отметить, что в реальных системах ШИхМ пульсации существуют практически всегда, так как даже в астатических системах при отсутствии опшбки от задающего воздействия имеется статическая опшбка от возмущений.

Установившуюся ошибку в типовых режимах удобно представлять в виде суммы

Ху {е) = Ху +х(Е), (23.61)

гдеХуст - постоянная составляющая; д- (е) - пульсируюгцая составляюп1ая.

Составляющая Лу определяется сравнительно просто, так как в установившемся состоянии ири Уу < 1 систе.ма с ПШМ по супюству превращается в линейную дискретную систему с передаточной ([зункцией приведенной линейной части (23.58). Выражения для х., приведены в работе [57]. Так, для рассмотренной в примере 1 системы cIIIUM-l

QV V

если kh > V. Если же kh < V, то Ууст 1. скорость из.менения управляемой величины Vy= kh< V, ошибка будет непрерывно увеличиваться, т. е. систе.ма станет неустойчивой.

11ульсиру ющую составляющую х(г) можно определить точно гак же, как это делалось в главе 14, или и;! уравнений (23.59). В частности, для той же системы с учетом выражения

x(e) = g(i + e)-y(i + E) = g{i + E)-g{i)-[y(i + E)-y(i)] и формул (23.62) получим:

f-e при0<е<1/3;

х(е) = <

[-0,5(1-6) при1/3<е<1.

Исследование устойчивости систем с ШИМ представляет собой гораздо более сложную задачу. Ее сложность, во-первых, состоит в том, что из-за наличия нульсаций асимптотическая устойчивость при строгом понимании смысла этого тер.мипа (гл. 16) .может быть обеспечена только при исчезающих вне1нпих во.здействиях, когда у.. = О и пульсации в установившемся состоянии отсутствуют. Однако, если амплитуда пульсаций находится в допустимых пределах, можно ограничиться исследованием асимптотической устойчивости в дискретные моменты времени t = iT.

Во-вторых, систе.ма с ШИМ остается нелинейной даже если в процессе управления широтно-импульсный модулятор ие насыщается, т. е. если скважность импульсов Yi< 1, что обусловлено нелинейностью уравнений (2,3..э1) и (23.57). При насьнцеппо.м модуляторе, когда у,- = 1, система с ШИМ при отсутствии внешних воздействий но существу превращается в систе.му с а.мплитудно-и.мпульсной .модуляцией, характеристика нелинейного звена которой имеет вид (23.23). В ней .могут существовать периодические режимы, рассмотренные в § 23.2. При наличии внешних воздействий при У; = 1 систе.ма может стать неустойчивой.

В-третьих, устойчивость системы с ШИМ (как и многих других нелинейных систе.м) зависит от величины и характера из.менеиия внешних воздействий.

Для иллюстрации отмеченных особенностей вновь обратимся к простейшей систе.ме, рассмотренной в при.мере 1. Для нее можно получить следуюпию точные условия асимптотической устойчивости в дискретные моменты времени [57J:

- при отсутствии внешних воздействий

<2, Yv<t=0;

1-khT-2, V= 5 c-i; 2 -khT= 3, V-5 с ; 3 - khT 3, V= 0; 4-khT= 1,5, 1=20 0-1