Таблица 14.2

Вид процесса

Белый шум

;?(0) 5(т) == Dboim)

Случайный процесс с ограниченной полосой

\тТ.

D2zsh:-Т

22-2zch--.- + l

2>

... +iY, - 4 T.

> T

Нерегулярная качка

z(z-dcosT)

dz(dz-cosT) dz-2zdcosT + l

2 2

sh --i-sm - -

1-b.sh --sm

Ifsh-tT- ,., 2

p7--sin -2 2

Прохождение сигнала через линейную систему. Пуст1> на входе линеЙ1Ю10 звена с и.звестной дискретной передаточной функцией W{z) действует случайная функция для которой известны корреляционная функция и спектральная плотность

5,(0)) или Sl(k). Тогдадля выходной величиныз.2(г)> аналогично непрерывному случаю, \южпо найти снектр;и1ьную плопюсть умножением снектрачьной плопюсти входного сигнала на квадрат модуля частопюй передаточ1К)й функции:

52(co)=M/(e>)p5i(0)), Sl(k)=\W\jX)\ S;(k). (14.133)

Интегрирование спектральной плотности по всем частотам в соответствии с

(14.128) и (14.129) позволяет найти средний квадрат выходной величины х?((). Это

по;шоляег для замкнутой импульсной системы производить расчеты, аналогичные изложенны.м в §11.8. Так, например, пусть в схеме, изображеииой на рис. 14.7, па входе действуют 1юлезный сигнал g(f) и помеха n{t), не коррелированные между собой. Обозначим их спектральные плотности 5g(X) и 5*(Х). Тогда спектра.чьпая плотность опшбки

5ЛХ)=\Ф\.{Гк)\ 5;(Х)+Ф(Д)Р S (k),

(14.134)

где Ф*(/Х) и Ф* (jX) - частотные передаточные функции замкнутой системы и замкнутой системы по ошибке.

Интегрирование (14.134) по всем частотам в соответствии с (14.129) дает средний квадрат ohhi6kh

Подобны.м же об)азом .могут быть найдены расчетные формулы н для других возможных случаев (см. §11.8).

Глава 15

ЦИФРОВЫЕ СИСТЕМЫ § 15.1. Общие сведения

Цифровой системой, как отмечалось в главе 1, называется система авто.матического управления, в состав уиравляюн(его устройства которой включена ци()ровая вычислительная MaiUHiia или специализированное цифровое вычис;н1тельное устройство. В дальнейшем будем сокращенно обозначать их как ЦВМ.

Пеггосредственно в целях управления ЦВМ используется для фор.мировапия про-гра.мм управления (§2.1) и цифровой реализации алгорит.мов управлеиня (§ 2.2) или корректирующих средств (§ 10.1).

Как правило, целесообразно вводить ЦВМ в систему управления в тех случаях, когда для решения указанных задач требуется сложная обработка инфор.мации или выполнение таких операций, которые не могут быть осуществлены с требуе.мой точностью при помощи аналоговых средств (умножение, деление, преобразование координат и т. п.). Это относится, например, к программам наведе1И1я типа (2.8), нелинейным алгоритмам управления, алгоритмам са.мопастройки и другим.

Вместе с тем в ряде случаев вполне оправданной оказывается цифровая реализация линейных корректируюпщх средств, которые обычно выполняются с исиользова-ние.м R-, С-, /.-элементов. Это свя.зано с тем, что характеристики таких элементов изменяются с течение.\г времени и под влиянием вненших факторов, а их надежность сравнительно невысока.

По.мимо непосредственного участия в управлении обт)ектом ЦВМ может выполнять такие операции, как контроль состояния элементов и устройств систе.мы, самоконтроль и др.

В общем случае иа ЦВМ может возлагаться ренгение задач с обслуживание.м нескольких зависимых или независимых каналов управления с разделением функций Зправлепия между ними по времени или по приоритету 93].

Один из вариантов функциональной схе.мы цифровой систе.мы авто.матическо1о управления при наличии двух кaнaJЮв показан на рис. 15.1. Управляемые величины г/.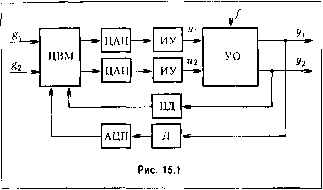

иг/2 измеряются соответственно аналоговым датчиком Д и цифровым датчиком ЦД. Так как ЦВМ оперирует пе с аналоговыми величинами (токами, напряжениями), а с числовыми (цифровыми) кодами, в систему вводится преобразователь аналоговой величины в цифровой код АЦП. Для связи ЦВМ с апалоговььми иснол-нительпыми устройствами ИУ используются преобразователи цифрового кода в аналоговые величины ЦАП. Задающие воздействия g, Hg2 формируются самой ЦВМ в виде программы управления или вводятся в нее извне. В последнем случае преобразования этих воздействий в цифровые коды осуществляется преобразователями АЦП. Футсции сравнивающего устройства, как правило, возлагаются па ЦВМ. Кроме исполнительных устройств в систему могут входить и дру1 ие аналоговые устройства, например, усилители,

ЦВМ представляет собой устройство дискретного действия. Это связано с тем, что решение задач управления осуществляется в пей путем вьшолнеиия арифметических онера1и1й. Поэтому в отличие от непрерывных систе.м реализация ею (ЦВМ) а.,И о-ритма управления происходит не мгновенно, а за конечный промежуток времени т. Ины.мм словами если информация поступает на вход ЦВЛ4 в момент вре.мени t = t, то результат вычислений .может быть получен лишь при t=c+T. Величина т зависит от сложности алгоритма и быстродействия ЦВМ. К пей добавляется еще и время, затрачиваемое на преобразования в ЦАП и АЦП.

Таким образом, результаты реализации алгорит.ма управления ЦВМ может выда-ватьлншьдискретно.т. е. в моменты времени? = П\ i = 0,1,2,причем Т>х. Значения т и Гмогут быть различны.ми для каждого из каналов.

Па основании и.зложенного, структурную схему одного кана 1а цифровой системы ( при условии независимости этого капала от других) можно представить так, как показано на рис. 15.2. При этом полагается, что ЦВМ реализует линейный алгоритм управлепия, а суммарное время .запаздывания тотнесено к непрерыв1К)й части системы.

Процесс нреобра,зовапия аналоговой величины g(;:) или y(t) в цифровой код g или у , осуществляемый АЦП, можно условно представить состоящим изтрех операций; квантования по времени, квантования по уровню и кодирования.

Квантование по времени возникает из-за того, что информация вводится в АЦП по команда.м, ноступающи.м от ЦВМ, липгь в .моменты времени t = iT. На рис. 15.2 эту операцию выполняют Kjn04H.

В процессе квантования но уровню весь диапазон измене1П1Я непрерыв1ЮЙ величины, например yit), разбивается на р., равных частей (квантов). Величина

g Утих Утт Hi

(15.1)