системы корни харакгеристического уравнения (14.88) или (14.89) до.-1жны находиться внутри круга единичного радиуса на плоскости z. По той же причине неприменимым оказывается и необходимое условие устойчивости, требуюптее положительности коэффициентов характеристического уравнения. Нанри.мер, в уравненин 2 - 0,5 = О один коэффициент отрицательный, однако корень 2, = 0,5 находится внутри круга едииич-пого радиуса.

Принадлежность корней к кругу единичного радиуса .может быть установ.тепа при по.мощи критерия Шур-Кона [90]. До некоторой степени он анатогичеп критерию Гурвица, однако при его пспользовапни необходимо составлять и анализировать определители вплоть до определителя порядка 2гг х 2п, где и - порядок характеристического уравнения. Поэто.му па практике этот критерий при.меняется редко.

Для того чтобы получить возможность использования для исследования устойчивости импульсных систем всех критериев устойчивое ги непрерывных систем, необходимо отобразить круг единичного 1)адиуса с плоскости z на левую полун.москость некоторой новой переменной. Для этого можно, например, нри.мепить рассмотрен1юе выше конформное 1треобра;ование ze . Однако в результате такой замены У1)авнепие (14.88) станет трансцендентным. Вместе с те.м в теории функций комплексного переменного существует преобразование

2 = i±i, (14.90)

которое называется билинейным, пли ж-преобразованием. Оно тоже отображает Kjjyr единичного ра;щуса палевую полуплоскость, по уже не плоскостир, а плоскости переменной гс.

Рассмотри.м, например, характеристическое уравнение (14.88) при п {. После подстановки (14.90) получи.м:

(До- !) + о+ 1 = 0- (14.91)

Для уравнений первого и второго порядка, как показано в главе 6, необходимое и достаточное ycjmBHe устойчивости сводится к требованию иоложительпости коэффициентов. Таким образом, условия устойчивости и.мпульсной системы при п = 1 имеют вид

ао- ,>0;1 2)

оц-ьа, >0.

При и 2 характеристическое уравнение и условия устойчивости следующие: (яц - а, -i- a2)i(-? + 2(ац - з) -ь a + а, -i- 20;

о - я, -I- 2 >

0() - 2 > 0;

о -I- 1 -(- 2 > 0.

При п = 3 кроме положительности коэ(})(зппиепговло.тжно дополнительно ньто.т-ияться условие критерия Гурвица (см. ivi. 6). Поэтому для исследования устойчивости требуется проверить выполнение пяти перапенств:

Зац - а, - 2 + Зй;, > 0; Зйц + а, - 2 - 3 з > 0; а + а, + 2 + rt.i > 0;

(14.94)

При п>4 условия устойчивости становятся слипп<ом 1ромоздкими. в качество примера исследуем устойчивость замкнутой системы, передаточная фугисция иенрерывной части которой

(14.95)

/г р

В соответствии с (14.60) при помощи таб;1.14.1 на.ходи.м передаточную функцию разомкнутой системы:

2 (2-1)

2 + 1 КтТ кг

г + -

-1-1

2-1 2 (2-1)2

Характеристическое уравнение замкнутой системы (14.89) и.меет вид

(14.96)

+ КтТ-2

2 + -

2

-КтГ + \ = 0.

Из неравенств (14.93) нолучае.м условия устойчивости замкнутой системы:

КхТ<2,

т>-. 2

Для исследования устойчивости за.мкнутых систе.м удобно использовать критерий Найквиста (см. г.т. 6). Чтобы построить амилптудпо-фазовую характеристику разомкнутой системы можно исполь.зовать преобра.зование 2 = еПоложивр =7(0, получим:

2 = е> =

= соя(Х)Т + jA\n(X)T =

шУ

(14.97)

Подставив (14.97) в выражение для передаточной функции разомкнутой систем>1 W(z), найдем частотную передаточную функцию ра.зо.мкнутой системы W(e ). Определив модуль и фазу и;!И вешествонгую и мщтмую части этой 4)упкцйи, можно построить а. ф. X. разо.мкнутой системы.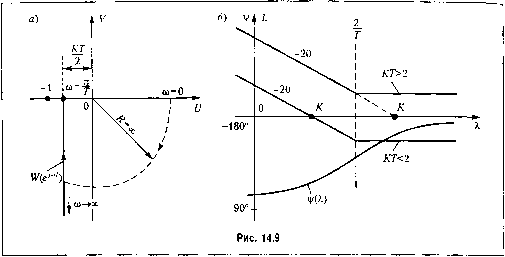

Следуетучитывать, что функция (14.97) периодическая. По.это.му при построении а. ф. X. достаточно о1раничиться диапазоном частот О < w < п/Т.

В качестве при.мера рассмотрим систему, передаточная функция непрерывной части которой

Wo{p) = K/p.

В соответствии с (14.GO) находим передаточную функцию разомкнутой системы

(14.98)

В результате замены (14.97) получим

4 /

l-7tg-2-

КТ .КТ (лТ

А. ф. X. разомкнутой (системы изображена па рис. 14.9, а. Так как при со = О она имеет разрыв, обусловленный наличиемр в знаменателе Wip), дополняем ее четвертью окружности бесконечно большого радиуса.

Для исследования устойчивости замкнутой системы можно использовать любую из приведенных в главе 6 формулировок критерия Найквиста. В знаменателе передаточной функции Wq(j}) пет корней с положительной веществеппой частью, т. е. / = 0. Поэтому в соответствии с первой ({юрмулировкой а. ф. х. разомкнутой системы не должна охватывать точку (-1 ,jO). Следовательно, как видно из рис. 14.9, а, замкнутая система устойчива ири КТ< 2. В соответствии со второй (}х)р.мулировкой сумма переходов а. ф.х. через критический отрезок должна быть равна пулю. npH7iT< 2 переходов нет и замкнутая система устойчива. При КТ> 2 а. ф. х. заканчивается на критическом отрезке, т. е. имеет .место -1/2 перехода.