Обратные связи. Такое со-елниеиие звеньев изображено на рис. 5.4. Обратная свя.зь может быть положительной, если сигнал .Тз, снимаемый с выхода второго звена, суммируется с сигнатом 1 на входе, и отрицательной, если Хз вычитается.

Для определения результирующей передаточной функции такой ко.мбииации звеньев запишем следующие очевидные соотношения:

.г-2=1У,(р)[х, ±.тз1; .X:=W2(p)x.

где знак плюс относится к положительной, а :щак .минус - к отрицательной обратной связи.

Решая эти урашюния совместно относительноXj, .можно найти результирующую передаточную функцию: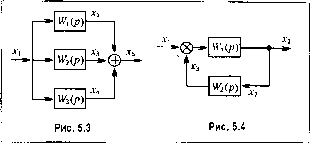

l + W,ip)W.,(p)

(.5.29)

B,ip)C2(p)

Ciip)C2ip)+B,ip)B,(py

(5.30)

Здесь знак минус относится к положительной, а знак плюс - к отрицательной обратной связи.

Обратные связи будут рассмотрены подробно в главе, посвященной .методам улучшения динамических свойств системы автоматического управления.

При использовании динамических звеньев обычно наиболее просто находится передаточная фупк1и1я разо.мкнутой системы (рис. 5.1). .Затем по фор.мула.м, приведенным в § 5.2, легко находятся все уравнения системы автоматического управления.

При анализе системы автоматического управления необходимо составить ее так называемую структурную схему, представляющую собой совокупность динамических звеньев со связями .между звенья.ми. Такая структурная схема часто является весь.ма простой и ее составлетше ие представляет особого труда. Однако в некоторых случаях составление структурной схемы сопряжено с большими трудностями и .может быть сделано только на основании детального анализа исходных диффере1щи-альных уравнений системы. В этом случае структурная схе.ма не облегчает нахождения основных уравнений системы, однако и в этом случае она остается весьма ценной, так как на ней в наглядной форме представлены все у:}лы исследуемой системы и все существующие между ними свя:т. Это .может оказаться полезным во всех дальнейших исследованиях.

На рис. 5.5 в качестве при.мера приведена ст])уктурная схема разомкнутой системы в том случае, когда цепь управления представляет собой простую цепь носледо-

a I-

РИС. 5.5

Рис. 5.6

вательно включенных звеньев. В .этом случае передаточная функция разомкнутой системы

Wip) = W,{p) Wip) Wip) Wip). (5.31)

Здесь WqCp), W\(p), 2(Р) и зСр) представляют собой заданные передаточные функции объекта и отдельных звеньев, входянцгх в систему управления.

Нетрудно видеть, что для нахождения передаточной функции разомкнутой системы можно разомкнуть систему пе обязательно так, как это показано на рис. 5.5, а в произвольном месте.

На рис. 5.6 изображен более сложный при.мер системы автоматического управления. Передаточная функция разомкнутой системы в этом случае

\ + W,{p)W,{p)

%{Р)-

(5.32)

И в этом случае для нахождения передаточной функции разомкнутой систе.мы можно разомкнуть систему в друго.м .месте, напри.мер в точках а, Ь, с или d.

Для рассмотренных иа рис. 5.5 и 5.6 систем, зная передаточную функцию разомкнутой системы W(jj), легко найти по формулам (5.18) и (5.19) дифференциальные уравнения для управляемой величины и ошибки;записанные в символической форме:

l + W(py

\ + Wip)

где g(t) - задающее воздействие.

На рис. 5.7 изображена структурная схе.ма систе.мы стабилизации. В этом случае задающее воздействие g(t) = const.

Определив передаточную функцию разомкнутой системы

W{p) = W,(p) Jfl Шр\ 1 + Ж,(;?)1Уз(р)

(5.33)

можно по формулам (5.18) и (5.19) получить символические записи дифференциальных уравнений для управляемой величины:

y(t.) = -LlLl-f{t), 1 + W{py

а) ! 2

Управляемый объект

1 l2

6) 2

4 3

в) 2

Рис. 5.7

Рис. 5.8

и ошибки:

х(0 = -

/(0.

где/(f) - воз.мущение, деГктнующее на объект, а W{p) - передаточтшя функция объекта но возмущению.

В тех случаях, когда структурная схема оказывается сложной и содержит .много различных иерекрестных связей, .можно попытаться ее упростить и свести к простейшему виду, напри.мер к изображеипой па рис. 5.5. Преобразование структурных схем линейных систем делается иа основе некоторых правил, которые даны в табл. 5.2.

Иа рис. 5.8 изображены этапы упропения сложной структурной схемы па основе приведенных выше правил. При упрощении введены дополнительные передаточные функции, определяемые выражениями

Щ-2 =

ж+ws

Полученная в результате преобразования схема (рис. 5.8, в) уже относится к простейшим.

§5.4. Уравнения следящей системы

Рассмотрим следящую систему, принципиальная схема которой изображена па рис. 5.9. Задающим устройство.м является командная ось КО, вращаемая извне по произвольному закону = дДО- Этот угол должен повторяться на управляемом объекте УО, ось которого является исгюлннтельной осью ИО. Мощность, требуе.мая для вращешя КО, ничтожна, так как с КО спеплен только движок потенциометра П]. Мощность, которую может потреблять для своего врагцення управляемый объект.