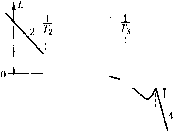С02 шо аШп М

Рис. 12.13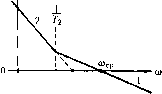

(1>2 ШО

Рис. 12.14

Допустить наличие такого множителя можно в том случае, если частота свободных колебаний звена значительно больн1е базовой частоты:

(12.8,5)

Асимптотическая л. а. х. для .этого случая изображена на рис. 12.13.

При выполнении условия (12.85) фазовый сдвиг, вносимый колебательным звеном в районе максимального запаса по фазе, можно принять равным arctg аю. Поэтому коэффициент а должен входить в общую сум.му постоянных времени (12.82) или (12.83).

Для того чтобы избежать появления второй запретной зоны в районе пика л. а. х. при ю = qQ (рнс. 12.13), необходимо вынолление дополнительного условия, которое вытекает из неравенства (8.87):

тос1(;о) = Л(%)<

М + 1

(12.86)

Выполнение этого условия может быть легко проверено при построении л. а. х. Более подробно этот вопрос рассмотрен для случая гироскопических следящих систем в [9].

Предельны.м случаем л. а. х. типа 2-1-2 или тИ1га 2-1-2-3 является л. а. х. типа 2-1 (рис. 12.14), соответствующая случаю, когда Z7-> 0. Тогда передаточная функция разо.мкнутой системы (12.81) приобретает вид

W(p) =

К,{\ + Т2Р) К,

(12.87)

Передаточная функция подобного вида соответствует изодромному управлению. Она может встречаться, например, в сглаживающих системах различного типа, построенных на ,электро,механических, электронных, гироскопических и тому подобных интеграторах.

Показатель колебательности для подобной передаточной функции может быть определен прямым отысканием максимума модуля частотной передаточной функции замкнутой системы

1+1У(;ю)

Подстановка (12.87) и исследование получивнюгося выражс1гия на максимум дает следующее условие, которое должно быть выполнено, чтобы показатель колебательности не превышал заданного значения:

Т2>

или, в другом виде (при условии, что со,. > Юо),

Т2>

2 М-Му1м-\

(12.88)

Типовые л. а. х. систем с астатизмом первого порядка. Следящие систе.мы с астатизмом первого порядка представляют собой наиболее распрострапеггпый тип систе\г, содержащих одно интегрируюпюе звено - исполнительный двигатель. В про-стейше.м случае, когда следящая систе.ма состоит из безынерционного усилителя и исиолнителыюго двигатстя с постоя1И1ой времени Г и пе имеет дополнительных корректирующих средств кроме, возможно, жесткой тахометрической обратной с;вя-зи, передаточная функция разо.мкнутой систе.мы может быть сведена к виду

Асимптотическая л. а. х. типа 1-2, соответствующая этой передаточной функции, изображена на рис. 12.15.

Определение допустимого значения постоянной вре.мешг может бьггь сдела1К) прямым нахождением .максимума амплитудной частотной характеристики замкнутой системы

W{Ja))

l + lV(;co)

= М.

Подставляя (12.89) и исследуя получившееся выражение на максимум, можно найти условие Того, чтобы показатель колебательности не превышал заданного значения: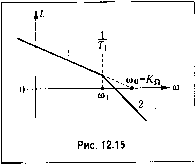

Последняя формула позволяет при заданном значении постоянной времени исполнительного двигателя легко определять максимальное зпачепие добротности по скорости, которое можно иметь в следяп1ей системе при данном значении показателя колебательности.

При заданном значении требуемой добротности по скорости эта же формула позволяет определять допустимое значение постоянной времени исполнительного двигателя и необходимый коэффициент передачи по петле жесткой тахометрической обратной связи, служащей для снижения постоянной времени двигателя. Определение коэффипиента передачи для тахометрической обратной связи может производиться по фор.муле

Т,=-

где Г., - постоянная времени испол1Н-1тельиого двигателя; k - коэффициент передачи но петле тахо.метрической обратной связи.

В более сложно.м случае передаточная функция (12.89) может быть представлена в виде

Щр) =

РО + Г,р)(\ + Т2Р)(\+Т2Р)...

(12.91)

Этой функции соответствует л. а. х. типа 1-2-3-4...

Здесь может быть получена приближенная формула, ориентировочно связывающая сумму всех постоянных вре.мени с добротностью по скорости:

К{Т,+Т,+Т,+...)<

(12.92)

приМ< 1,3.

Приближенная формула (12.92) становится точной при М = 1 и любом числе постоянных вре.мени либо при наличии только одной постоянной времени и любом значении М. В последнем случае она вырождается в формулу (12.90). При значениях М, мало отличающихся от едини1П>1, например при М < 1,3, формула (12.92) является достаточно точно!! и может использоваться для расчета при наличии любого числа

П0СТ0Я1П1ЫХ времени, а также при на.;1ичии временного запаздывания т, которое должно учитываться в общей су.мме постоянных времени.

Л. а. x. рассмотренного типа может исполь- зоваться в простейших следящих системах с невысокими требованиями в отношении статической и дипа.мической точности. При невоз-.можности удовлетворить требования.м технического задания приходится переходить к более сложным типам л. а. х. На рис. 12.16 изображена асимптотическая л. а. х. типа 1 -2--1-2-3... Она может быть получена из соответ-