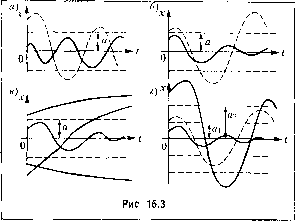Процессы в нелинейных системах авто.матического управления и.меют целый ряд весьма существенных особсшгасгей, которые не встречаются в линейных системах.

Благодаря эти.м существенным особенностям даже вопрос об устойчивости системы становится здесь более слож1Н)1М. Кроме структуры систе.мы и значений ее параметров л-тя устойчивости того или иного устаповив1пегося процесса в отличие от линейных систем и.меют значение также и начальные

условия. Возможен новый вид установившегося процесса агвтоколебания, т. е. устойчивые собствеиные колебания с постоянной амплитудой при отсутствии внешних колебательных воздействий. Когда в системе возникают автоколебагитя, то установившееся состояние, соответствующее постоянному значению управляемой величины, становится невозможпы.м.

Следовательно, в общем случае па плоскости параметров системы .могут быть не два вида областей (устойчивости и пеусто1!Чнвости), как в линейных системах, а больше: 1) область устойчивости равновесного состояния с постояиньгм значением управляемой величины; 2) область автоколебаний; 3) область иеустойчивости с;истемы; 4) области, соответствующие другим, более сложным случаям.

Если пропсссы в систе.ме и.меют вид, ука;!аи}П11Й па рис. 16.3, а, то равновесное состояние (х = 0) неустойчиво. В том случае, когда оба указанных па рис. 16.3, а ко-лсбатпш в переходных процессах стремятся к колебапия.м с одной и той же амплитудой и с одной и той же частотой, система будет об.тадать автоколебаниями с а.чшлитудон а. На рис. 16.3, б и б показаны случаи, когда равновесное состояние (х = 0) системы устойчиво в мало.м , т. е. ири начальных условиях, ие выводящих отклонения в переходном процессе за определенную величину й, и неустойчиво в большом , т. е. при нача,чьных условиях, выводяпщх отклонение в переходном процессе за пределы величины а. Здесь грагпчпы.м процессом является неустойчивый периодический процесс собственнс)го двггжепия системы с амплитудой а (переходные процессы расходятся от пего п обе стороны).

На рис. 16,3, г показан стучай трех воз.можных устаповивнитхся состояний: 1) равновесное состояние (х = 0); 2) колебагитя с постоя1Гпой амплитудой а,; 3) колебания с постоянной амплитудой а-. При .это.м колебания с а.\н1Литудой а, неустойчивы. В результате систе.ма будет устойчива в малом ио отношегнпо к равновесному состоянию X = О, а в большом система будет обладать автоколебагтями с амплитудой 2-

П р и м е р. Лля иллюстрации особенностей нелинейной системы исследуем переходный процесс и автоколебания в релейной системе стабилизации температуры. Для этого состави.\1 снача-та уравнения управляемого объекта и унравляюнтего устройства.

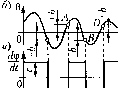Рис. 16.4

Пусть об1>ект представляет собой некоторую камеру. Уч1ггывая иперци-oiHiocTb пропесса нагрева и охлаждения, запиндем его уравнение в виде

1 + 0 = -М + /(О, (16.9)

где О - о1 ivionenne температуры; ф - отклонение управляющего органа, f(t) - впетпие возмун1ения.

При отклонении температуры G появляется ток в диагона.ти .моста того или иного направления и за.мыкается соответ-ствуК)Н1ИЙ контакт реле, включаюнтего постоянное напряжение в ту или иную обмотку возбужде1Шя электродвигателя. Приняв во в1Н1манпе некоторое отставание в этом процессе включения, получим релейную характсрнстшсу Далее, считая, что ток / про-

порционалсп отклонению те.мпе15атуры объекта 0, а скорость - отклонения управляющего органа пропорциональна нап{)яжснию на об.мотках возбуждения электродвигателя, можно в данном случае выходной величиной для указанной релейной характе-

ристики считать прямо -, а входной - 6 (рис, 16.4, а).

Следовательно, уравне1Н1е управляюнюго устройства запишется следуюпщм обра-

зом:

б/ф It

= +с при Q>+b, = -с прн 0<+6,

когда

dQ dt

>0;

(16.10)

~ = ч-с при Q>-b, dt

d<p

= -c при 0<-b,

dQ

когда T~< -dt

(16.11)

Рассмотрим два произвольных участка переходного процесса (при/(£) = 0) в данной системе (участки АВ и BD па рис. 16.4, б).

На участке АВ уравнение уи1)авляюн1его устройства согласш) ihic, 16.4, в будет

- = +С- Дифференцируя (16.9) по t и подставляя туда +с, получаем при/(0 = О

следующее уравнение системы на участке АВ:

dQ do

dt dt

а па участке

Решение уравнения (16.12) будет

и -- + - =+кс.

= С,е -k,c,

откуда получаем

(16.13)

(1(5.14)

(16.15)

Усл(изи.мс:я для простот1>1 отсчитывать вре.мя toT начала участка yli5 (рис. 16.5, а). Тогда начальные условия будут

9 = +6, = 9л при t = О,

где 0 пока неизвестно. Используя начальные условия, находим произвольные постоянные для уравнегп1я (16.15):

С=9+А;,с, C2=6 + 7Ci. (16,16)

Аналогично для участка BD согласно (16.13), отсчптьшая вре.мя t тоже от начала .этого участка (рис. 16.5, б), получим решение

f = C;e~- +к,с,

9 = -Г,Се i +kct+C,

(16.17)

Все остальные участки кривой переходного процесса будут определяться, очевидно, такими же решетгия.ми, по только с другими

:Ц1ачепиями величин С С, 9д , С Сз, 9 . Заметим, что величины и 9, необходимые для определения [фоизвольных пост оян-ных, находятся как значения 6 в конце нредшеству10П1ИХ и.м участков. Поэто.му, если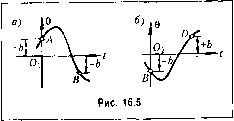