Приближенный колшлексный коэффициент усиления, или нриближеннал амплитудно-фазовая характеристика нелинейного зненас уравнениемл2 = /(.г,), при наличии гистерезисной пет;ш, следовательно, будет

W,=q{a) + jq{a),

(18.210)

а без гистерезисной петли

W,{a)=q{a).

(18.211)

Эта характеристика определяет ам[1литуду и фазу первой гармоники на выходе нелинейного звена (если на его вход подается синусоида), а именно выражение (18.210) можно представить в виде

W,(a) = A,( )e*< >,

A {a) = [q{a)f+[q{a)J, р (а) = arctg.

(18.212)

Следовательно, амплитуда ие[)ВОЙ гармоники иа выходе будет 2 °° аЛ {а), а фазовый сдвиг - Р (а), где а - амплитуда иа входе нелинейного звена. В результате получи.м следующие вынужденные колебания на выходе нелинейного звена (первая гармоника);

л-2=аЛ (д)51псог+р (а)1.

Например, выходная величина 2 релейного звена с характеристикой рис. 18.1, а меняется в ироцессе вынужденных колебаний по :?акону, изображенному сплошной ломаной линией на рис, 18.38, в. Пунктиром [юказана основная синусоида для нес, причем из (18.212) и (18.15) имеем;

. Ас . v-j-Vi 2сV2

2 =аЛ.. =-sin-=-- =-

л 2 л

2 2)

= -arctg

Действитсльпая ступенчатая кривая .заменяется в даппо.м случае синусоидой (первая гар.моника), вершина которой совпадает с осью симметрии действительного прямоугольника (рис, 18 38, в).

Для нелинейных звеньев с уравнением видаХ2 = f (х,) без гистерезисной петли, как следует из § 18.1, 9 (а) = 0. Следовательно, для таких звеньев Л (а) и Р = 0,т. с, вынужденные колебания на выходе пе имеютс})азового сдвига.

Масипаб для кривых Л 2 3 4 5

Одним ИЗ главных отличий вынужденных колебаний нелинейных систем от линейных является их супюственная зависимость не только от частотьг, но и от амплитуды входных колебаний. Эту главную особенность как раз и улавливает на1И5санное здесь приближенное выражение амплитудно-фазовой характеристики нелипейногозвена. В формулах (18.210)-(18.212) получилась зависимость только от ам[1литуды а, пото.му что офани-чились рассмотрением только нелинейности вида = f (-v,). Для более сложных нелинейных звеньев в амплитудно-фазовую характеристику войдет также и частота ю. Кроме того, как увидим ниже, зависимость от частоты будет всегда вводиться линейной частью системы.

В § 18.1 были приведены выражения q (а) и q (а) для наиболее типичных релейных и других просгейишх нелинейных звеньев. Иа основанирг этого строятся приближенные амплитудные и фазовые характеристики путе.м вычислений по формулам (18.212). Результаты для простейших случаев приведены нарис. 18.39 и 18.40. Та.м приведе[1Ы также и обратные амплитудно-фазовые характеристики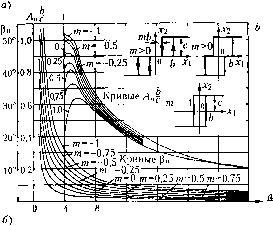

\2 16 20 Масштаб для кривых Рн

m- 0,75 m=-0,2.5/m=0,5

m=-l

m=-0,5

=0,25

=0,75

Рис, 18,39

М,Да) =

= X {a) + jY,ia).

(18.213)

Ha графиках указаны все необходимые обозначения и типы нелинейных характеристик звеньев. Аналогичным путем .можно построить графики и для других конкретных нелинейных звеньев.

Амплитудно-фазовая характеристика линейной части системы согласно (18.206) имеет вид

Q(7to)

(18.214)

Общая приближенная амплитудно-фазовая характеристика всей разомкнутой системы с нелинейным звено.м будет

1У(а,ш) = (я)1У, (Ую) = [q(a) + jq(a)]W, (jw).

(18.215)

Следовательно, амплитуда и фаза первой гармоники выходной величины х, определяемые фор.мулами

а-, =

б) л

1,0 0,8 0,6 0,4 0,2

рн-0-

И 13

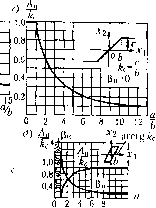1012b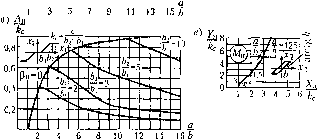

И P3=argW(a,co), (18.216)

зависят .здесь не только от частоты ю, как в линейных системах, но enie и от величины входной амплитуды а.

Отыскание автоколебаний замкнутой системы. Незатухающие синусоида-ч ьныс колебания с постоянной амплитудой в замкнутой системе определяются согласно критерию устойчивости Найквиста (см. гл, 6) прохождением амплитудно-фазовой характеристики разомкнутой системы через точку (-1, jO), т. е, равенством IV = -1. Это и будет в данном случае условием существования периодического решения для замкнутой нелинейной системы, которое приии.мается приближенно синусоидальным. Итак, и.меем условие

W{a, со) = -1.

Учитывая (18.215) и (18.213), это можно записать в виде

1У,(;ш) = -М (а)

Рис. 18.40

(18.217)

1У,(7Ш) = -

q{a) + jq{a)

(18.218)

где q (а) = О в случае отсутствия гистерезисиой петли (правая часть (18,218) в этом случае будет вещественной).

Левая часть уравнения (18.218) или (18,217) представляет собой амплитудно-фазовую характеристику линейной части системы, а правая - обратную амплитудно-фазовую характеристику нелинейного звена (для первой гармоники), взятую с обратным знаком. Ре1пение этого уравнения можно получить графически как точку иересе-