показать, что процессы, подобные изображенному па рис. 14.5, б, будут исключеиы, если

1 гг-ту п

Специфической особенностью импульсных систем является возможность существования в 1HIX переходных процессов конечной длительности, полностью закапчивающихся за конечный промежуток вромепп t = kT,k= 1,2,... (рис. 14.10, б). Для этого параметры систе.мы должны бы гь выбраны гак, чтобы корни характеристическоп) уравнения (14.91) располагались в начале координат на плоскости z. Тогда передаточная функция замкнутой систе.мы принимает вид

Y(z) W(z) V*-4fei2-4... + V,i G(z) 1 + Wiz) z

Ф() = 7;7Т=. - , (14.106)

Ей соответствует разностное уравнение

уИ) = hig{i ~ 1) + b,g{i - 2) + Ь,. ,g(/ - k) (14.107)

При подаче на вход системы единичного ступенчатого воздействия и г/(0) = О получим:

г/(1) = г о, y(2) = ho+b, yik) = bo+b+... + bk i,

y(k + \) = y(k + 2) = ... = yik). -

Например, в системе с передаточной функцис!! (14.98) можно получить процесс с г = 7, если КТ= 1, а в системе с передаточной функцией (14.96) - процесс с f = 2Г, если Г2-1,7СтГ=1,.5.

Следует однако учитывать, что системы с процессами коггечпой длительности часто имеют .малый запас устойчивости. Так, во втором из рассмотренных случаев при указанных параметрах передаточная функция (14.96) имеет вид

G(z) z

Из (14.108) находим: i/( 1) = 2, i/(2) = у(3) =...= 1. Таким образом, неререгулирова-пиеа%= 100%.

Запас устойчивости по амплитуде и по фазе и показатель колебательности замкнутой системы для и.мпульсиых систем определяется точно так же, как и для иепрерыв-ных систем (§ 8.8). Отличие состоит только в виде частотных характеристик этих систе.м.

Рассмотрим, например, систему, передаточная функция которой в разомкнутом состоящей имеет вид (14.96):

W(z) = ~ + (14.109)

2 (2-1) 2-1

Воспользуемся для расчета методом логарифмических частотных характеристик. С зтой целью в (14.109) сделаем подстановку (14.99). В результате получим частотную передаточную функцию разомкнутой системы

К{\ + JAT)

1- JA-

(14.110)

Ее модуль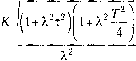

и фаза

Ц1{а) = -180° -I- arctgAT - arctg ХГ/2.

Ло1 арифмические частотные характеристики для с;1учая т > Т/2, КтТ< 2 изобра-же1П)1 иарис. 14.11.

Асимптотическая ;i. а. х. построена в соответствии с выражением (14.110). Ее первая асимптота имеет наклон -40 дБ/дек и пересекает ось абс1щсс па частоте Xq =

На сопрягающей частоте л = - она изламывается на-*-20 дБ/дек, а па частоте Х = ~ -

enie па -1-20 дБ/дек. При Х = <=<, модуль\Щ]Х)\ равен 0,5ХтГ. Поэтому при КхТ< 2 третья асимптота располагается ниже оси абсцисс. Таки.м образом, при т > Т/2 и КгТ < 2 за.мкнутая система устойчива, так как л. ф. х. не пересекает критический оТ1)езок. Запас устойчивости замкнутой системы по а.милнтуде (см. §8.8)

A,=201g

KzT .

(14.111)

Для определения запаса устойчивости ио фазе найдем частоту среза л. а. х. Х. В соответствии со свойствами треуголышков иа плоскости л. ч. х., гипотенузы которых имеют наклоны -20 дБ/дек и -40 дБ/дек, имее.м:

W{jX,)

К 0

к XV

Отсюда частота среза л. а. х.

(14.112)

Таким образом, запас устойчивости замкнутой систе.мы по фазе V, - 180 + v(Xo) = arcig - arctg X, Т/2.

(14.113)

Для определения показателя колебательности замкнутой системы М необходимо при помощи р-кривых (рис. 8.23) построить запретную область так, как показано на рис. 8.24. При этом параметры К,т и 7 должны быть заданы численно. В данном случае можно найти такие значения этих параметров, при которых будет обеспечено наперед задашюе значение показателя колебательности.

Нетрудно видеть, что случай (рис. 14.11) по расположению фазовой характеристики сводится к случаю л. а. х. типа 2-1-2, изображенной на рис. 12.10. Используя нолучептле в главе 12 формулы, получаем онти.магьную протяженность участка с па-клоно.м -20 дБ/дек:

2t MjH Т М-\

(14.114)

Базовая частота л. а. х. = [К. Далее имеем связь между постоянной вре.мени т и базовой частотой:

т = -

ло VM-r

откуда находим коэффициент передачи разо.мкнутой систе.мы

2 1 Л/ 4 М(М-1)

Эту формулу можно записать также в следующем виде:

КТМ(М-\)

(14.115)

(14.116)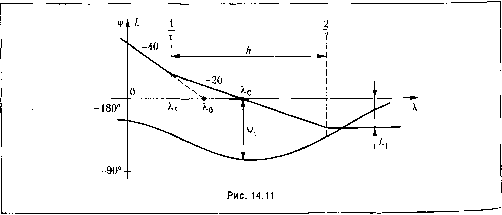