необходимо X за.менить найденной выше функцией (22.20). Тогда в уравнении (22.21) останется одна неизвестная величинаа. Учитывая формулы (11.91) и (11.92), уравнение (22.21) .можно .записать в виде

ai = hl ( X , Of),

(22.23)

где h - постоянный множитель, выносимый за знак интеграла (формулы для вычисления интеграла 1 приведены в приложении 1).

Таким образом, путем решения уравнения (22.23) с подстановкой (22.20) будет найдено среднеквадратичное отклонение а,а затем но формуле (22.20) будет вычислено и .математическое ожидание f, т. е. полностью определится иско.мое приближенное решение уравнения (22.15):

х + х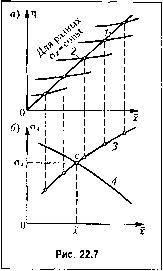

(22.24)

Это решение справедливо для случая уста1Ювившегося режима при стационарном случайном ироцессе.

Однако зависимость х (а) датеко не всегда можно выразить из уравнения (22.19) в явном виде ввиду сложности выражения F (х, а.). Поэто.му в большинстве случаев придется решать совместно два уравнения, (22.19) и (22.23), либо численно, путем носледовательных приближений, либо графически.

Можно применять, например, следующий графический прием. Представим уравнение (22.19) в виде двух уравнений:

5Х0)/ Ж( ). йФ) Q(0)

(22.25)

Первое из них дает прямую 1 (рис. 22.7, а), а второе - серию кривых 2 для различных постоянных значений х, о. Перенеся все точки пересечения этих кривых с прямой 1 на плоскость координат х , а(рис. 22.7, б), получим завнси.мость a,.( х ) в виде кривой 3, так как каждой точке пересечения на верхнем графике соответствовало определенное значение а,.. После .этого построим (рис. 22.7, б) еще одну зависимость

а.( х)в виде кривой 4 по формуле (22.23), подставляя в правую часть этой формулы

значения а, взятые для каждого х из кривой 3. Очевидно, что координаты точки пересечения С кривых 3 и 4 представляют собой иско.мый ре:!ультат совместного решения уравнений (22,19) и (22,23).

Во нссх задачах здесь н далее буде.м искать приближенное poHieiiHC только для iiepe.viennoii х, стоящей иод знаком пелипейиости. Когда оно майдемо, всегда .можно через соответст у1ом1ие иередаточ1н.1е функции найти приближенное реишние и для других переменных системы.

Вторая 3 а л а ч а. Перейдем теперь к реше11ию другой задачи, когда ис-с;1едуется пеустаиовивщийся процесс.

Часто в автоматических системах управления разложению искомого рете-иия (22.24) па х и х соответствует разложенце его па полезный регулярный сигнал .г и случайную помеху х . Когда полезный спгпа.! управления X изменяется во времени, процесс уже пе будет стационарным. Однако если помехи (флуктуации) характеризуются спектром значительно более высоких частот, чем полезный сиг-пал, .можно считать последний медленно меняющимся. Тогда .можно исследовать случайный процесс в первом приближении как стационарный, при.мепяя формулу (22.23). Но при .этом ;У1Я определения ритлярпой состав.1ЯЮ1цей х нельзя нолыюваться ачгебраи-ческим уравнением (22.19), а надо обращаться к днфференциальпо.му уравнению (22.17).

В этом случае описанное выше графическое решение ие годится и следует гюсту-нать иначе. Сначала надо из уравнения (22.23) определить зависимость о.( х ). Для .этого по аналогии с графическим peineimeM (21.25) разобьем уравнение (22,23) на два уравнения: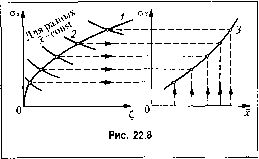

hl (x, Од.) = С

(22,26)

Первое из них дает параболу / (рис. 22.8), а второе - серию кривых 2 ирн разных постоянных :шачениях х. Перенеся ординаты их точек пересечения па плоскость х, и отложив для каждой из них соответствующие кривым 2 абсциссы х, !юлучи.м в виде кривой 3 (рис. 22.8) искомую зависимость о, (.v).

Подставив полученную зависи.мость х) в вычисленное для заданной нелинейности согласно § 22.1 выражение

Fix, а,), (22.27)

исключим из пего величину а. и получим функцию от заданной переменной

/ -Ф(х), . (22.28)

которую, как и в главе 19 и § 21.2, можно назвать функцией смещения, так как здесь .математические ожидания х и Р представляют собой смещения центра случайных составляюпщх,

Ко1-да функция смещения (22.28) найдена, ее .чюжпо подставить в урав1ЮШ1е (22.17): QiP) X + /г (/;) Ф (.V ) = 5 ip) f it), (22.29)

По аналогии с. нведенмыми рапсе функциями смещения это будет сглаженная при помощи случайных флуктуапни нелинейная характеристика для медле1н10 .меняющейся состаиляюн1ей процесса.

и отсюда по задатюй функции / (О найти путем решения дифференциа,тьпого уравнения ре1уляриую составляющую процесса x(t).

В больпшнстве задач функция смещения (22.28) будет и.меть вид плавной кривой (рис. 22.9), которую в некоторых пределах можно подвергнуть обычной линеаризации

= tg3.

.i=0

(22..S0)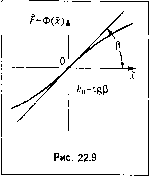

В случае, если систе.ма такова, что линейная часть с передаточной функцией

Q(p)

не пропускает спектр частот, соответствующий флуктуациям f {t) и определяемый спектральной плотностью sy((a), отыскавие величины а. значительно упроп1ается, а именно из (22.21) следует

5(;ш)

Q(;w)

i / (ш)/со.

(22.31)

т. е. не будет зависеть от формы пелинейностп и от величины х .

В этом случае вместо дифференцирования функции смещения (22.28) можно определить i пепосрсдственно из (22.27):

F - kjx, i -

Здесь k получается как функция от

А = k, (а,).

(22.32)

(22,33)

Затем надо подставить величину а,., найденную из формулы (22.31).

Вместо этого .можно воспользоваться кривой на рис. 22.3, 6-22.6, б, соответствующей найденному значению а.. При :-)том вычисление интеграла (22.31) производится но готовым формула.м aj. =/г/ (см. приложение 2).

В ре.зультаге подстановки (22.30) или (22.32) уравнеиие для определения pei-уляр-пой составляющей (22.29) станет линейным:

IQip) + k R (р)] .V = 5(р) 7 (О. (22.34)

Оно 1)ешается при помощи обычного характеристического уравнения

Q(j})+KR(p)- 0. (22,35)