Будем теперь рассматривать режим гармонического входного воздействия, в котором амплитуда скорости по-прежпему равна максимальному значению, а амплитуда ускорения меньн1е максимального. Тогда контрольная частота (12.47) будет пропорциона.;1ЬПо уменьшаться, а амплитуда (12.48) возрастать обратно пропорционально амплитуде ускорения. При этом контрольная точка Лк будет перемешаться влево по прямой, имеющей наклон -20 дБ/дек. В предельном случае, если принять а.милитуду ускорения равной пулю, контрольная частота со ~ О- Это соответствует режиму вращения с постоянной скоростью Qj = unux- Тогда формула (12.4,5) вырождается в известное соотнопюние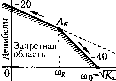

Рис. 12.8

(12.49)

где Kq fc ] - предельное значение добротности по скорости следящей системы с астатизмом первого порядка, ниже которого нельзя иметь реальную добротность по скорости, исходя из условий точности.

Если теперь рассматривать режи.м га]).монического входного воздействия с амплитудой ускорения, равной максимальному значению и амплитудой скорости, меньшей максимального значения j., то аналогичными рассуждепня.ми .можно показать, что контрольная точка (рис. 12.8) будет двигаться вправо по прямой, имеющей наклон -40 дБ/дек. Квадрат частоты точки пересечения этой пря.мой с осью нуля децибел раве}1 предельной добротзюсти следящей системы с астатизмом второго порядка по ускорению

. = е зУд, , (12.50)

равной отношению ускорения к установившейся ошибке. Это будет при условии, что первая асимптота л. а. х. проектируемой следящей системы совпадает с пря.мой, но которой движется контрольная точка А (рис. 12.8). Ниже этого предельного значения не может быть реальной добротности следящей систе.мы с астатизмом второго порядка.

Область, расположенная ниже контрольной точки А и двух прямых с наклонами -20 и -40 дБ/дек, представляет собой запретную область для л. а. х. следящей системы с астатиз.мом любого порядка. При работе со скоростями и ускорениями, не превышающими значетгй Qiax и imax- ошибки следящей системы пе будут превосходить значения , если л. а. х. будет проходить не ниже запретной области.

Для входного воздействия вида (12.43) можно также ограничивать фазовую и относителгтую амплитудную составляюпще оншбки. Для этого найдем опшбку 6, находящуюся в фазе, и ошибку 9ф, находящуюся в квадратуре по отношению к входному во.здействию. Для этого }ia рис. 12.9 построим векторную диаграмму, из которой следует

l + W(jcoJ

= {U + jV)Q,=Q+iQ, (12.51)

p = arctg = arctg - (i2.52)

О) о л 0( ,av Од ,а

и относительная амплитудная опшбка

(12.53)

Вформулах(12.51)-(12.53) и нарис, 12.9 величины 9 G2,6,9,, и95 представляют собой векторные изображения соответствуюпшх гармонических функций времени д д2-1*фИЛ-

В большинстве случаев, аналогично изложенному выше, можно считать, что !0м,<) 1 и передаточ1шя функция разомкнутой системы с астатизмом первого порядка в области низких частот имеет вид

7ю(1 + 7юГ,)

Тогда фазовая опшбка (при arctg ф = ф) на осповапии (12.51)

1 г Imiv W,c

Ф = -- п sir (12.54)

и относительная амплитудная опшбка Дд

. i Re-lliHiL = IZI.fi. 12 55)

,max Unax Ипах Ок) .

Задание величины фазовой и относительной амплитудной ошибок определяет предельные положения первой и второй асимптот л. а, х., т. е. необходи.мые значения добротности ИО скорости Kq и добротности по ускорению = Kq/1\. Нетру/цю видеть, что предельные положения асимптот и в этом случае фор.мируют запретную зону для низкочастотной части л. а. х. вида, изображенного па рис. 12,8. Исиользование нриведеипых выше формул для формирования низкочастотной части л. а. х. воз.можно лишь в том случае, если двигатель в состоянии обеспечивать получение па исполнительной оси требуемых максимальных значений скорости Qimax и ускорения гях

При выводе всех ириведепных выше ([юрмул предполагалось, что опшбка в системе определяется только наличием задающего воздействия (t). При действии на систе.му возмупюпий, например момента нагрузки иа оси двигателя, необходимо увеличение коэффициеита пс[)едачи разо.мкнутой системы для того, чтобы результирующая опи1бка не превосходила заданного значения. Более подробно это изложено, например, в 9J.

где UhV вещественная и мнимая части частотной передаточной функции но ошибке. Фазовая ошибка следящей системы

фшах -liiiax ~ Лшах

Пусть, кроме того, задано требуемое значение коэффициента оннгбки Cj, являющегося коэффициенто.м пронорциональпости между скоростью входного во.здействия и оншбкой.

Примем, что в низкочастотной области частотная передаточная функция статической системы может быть сведена к выражению

(1 + Г 70))(1 + Г,У(0)

Тогда коэффициент ошибки Cj для этой нередаточной функции будет равен

q=Zo Z.. (12.58)

Отсюда может быть получена допустимая сумма двух постоянных времени:

То+Т,<с,К = с,. (12..59)

Формулы (12.57) И (12.59) устанавливают требования к низкочастотной части желаемой л. а. х.

Если к проектируемой системе кро.\к! задаюп1его воздействия приложено воз.му-пюние, то в фор.муле для ко;)ффициецта передачи разо.мкнутой систе.мы необходимо дополнительно учесть составляющую, определяемую .этим возмущением. Пусть, напри.мер, статическая ошибка от воз.мушения определяется формулой (8.4):

\ + К К

где Yj - коэффициент статиз.ма, а /iq - постоянное воз.мущение.

В статических системах установившаяся ошибка по задаюпюму воздействию может быть сделана равной пулю применением неединичной обратной связи (§ 9.3), Однако появление статической ошибки возможно при пестабильпости коэффициента передачи разомкнутой системы; В соответствии с формулой (9.66) для рассматриваемого случая максимальное значение ошибки составит

Vmax - (12.56)

где -гг относительное изменение коэффициента нередачи разомкнутой систе.мы. л.

Из пыражеуигя (12.56) можно получить требуемые значения коэ4)фициента нередачи /Гили коэффициента ошибки Cq.