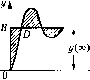Рис. 8.16

Наименьшее значение носледиего выражения будет при вьгполнеггии условия 7х + х = (7р + 1)л- = 0.

Это есть дифференциальное уравнение первого порядка, решение которого имеет вид

(8.73)

ГД Уо х - установившееся отклонение управляемо!! величины.

Этот процесс изображен на рис. 8.16 пунктиром. Следовательно, выбирая нара.метры системы но минимуму улучшенной интегральной оценки (8.72), можно приблизить переходный процесс к заданной экспоненте (8.73) с постоянной времени 7 , которая носит в этом случае название экстремали. Из этих соображений можно заранее задаться определенной величиной Т.

Выбор пара.метров системы по улучшенной квадратичной 1Н1тегральной оценке приводит к менее колебательным процессам по сравнению с использованием обычной квадратичной интегральной оценки (8.56).

Методика вычисления интеграла (8.72) сводится к тому, что правая его часть разбивается па два слагаемых:

I, = \x4t + Txdt.

При входном воздействии тина единичной ступенчатой функции первое слагае.мое последнего выражения соответствует интегральной оценке /, а второе - Т1. Поэтому для этого случая получаем

2 (8.74)

Улучшенная интегра-тьная оценка 4 может также применяться в безразмерном виде аналогично (8.57) и (8.68):

(8.75)

где Qq - среднегеометрический корень характеристического уравнения, а С - некоторая величина, и.меющая размерность г/(0, например статическое отклонение у{°°).

Недостатком приведенных расчетных формул для вычисления как /, так и 7 является их выражение через определители, которые трудно бывает раскрывать в буквенном виде ири высокой степени характеристического уравнения. В .этих случаях

можно использовать имеющиеся специальные приемы числовых расчетов. Сам определитель Д (8.62), как старший определитель Гурвица, согласно § 6.2 имеет вид

Д = Д = йз(й,а2 - Яоз) ри и = 3,

Д = Д = Й4[яз(й,а2-йойз)-<5Й11 , при и = 4,

А = А = Й5[(Я,Й2 - йоЯз)(йзЯ4 - Й2Й5) - (й,й - floflj)] при п = 5.

Несколько сложнее вычисляется только определитель А , когда первый столбец А (8.62) с одним элементом а за.мепяется столбцом (8.63) с двумя элементами а и a . Все остальные определители оказываются проще.

Удобство иптеграль?1ых оценок состоит в том, что они дают единый числовой критерий качества. Недостатком является то, что одному и тому же значению интегральной оценки могут отвечать разные формы переходного процесса, что создает недостаточную определенность реше1И1я задачи.

В принципе возможно исиоль.зование более сложных выражений, че.м (8.72), в которые кро.ме первой производной от отклонения будут входить вторая, третья и т. д. производные. Так, напри.мер, ограничившись при подаче ступенчатого воздействия g(0 или/(t) отклонением ж, первой производной x и второй производной x , получим иитефальную оценку в виде

l,=]{x+TxT,x)dt. (8,76)

Эта оценка будет характеризовать приближение переходного процесса к экстремали, определяемой решением дифференциального уравнения

Tx + Ti х + х = 0.

Экстре.маль в данно.м случае будет соответствовать более сложной кривой, че.м экспонента, что позволяет точнее задать желаемый вид переходного процесса. Однако нахождение интегральных оценок вида

I = I + lfl + Tr,

к которым сводится вычисление интеграла (8.76), сопряжено со значительными трудностями, что ограничивает их нриме?1ение.

Определение минимума интегральной оценки. Пусть требуется исходя из минимума какой-нибудь интегральной оценки, выбрать два каких-нибудь параметра а и 3 заданной автоматической системы. Указанные два параметра входят в коэффициенты дифференциального уравнения системы. Прежде всего по вышенрипеден-ным формулам находится выражение соответствующей интегральной оценки. Это выражение, если все пара.метры системы 3aiianbi, кро.ме а и 3> и.меет вид

/=/( , 3).

Для определения значений а и Р, соответствующих минимуму /, вычисляем частные производные по а и р и приравниваем их нулю. В результате получаем два уравнения:

da d

с двумя неизвестными а и 3. Отсюда и определяются искомые значения параметров а и р. Чтобы убедиться в том, что это действительно минимум, а не максимум, можно вычислить значение / при полученных значениях а и р, а затем при каких-нибудь соседних. Последние должны оказаться больпш. Аналогично можно поступить и при выборе нескольких параметров по минимуму интегральной оценки.

Функция / (а, Р) пе всегда обладает минимумом но рассматриваемым параметрам. Тогда нужно выбирать их по паи.меныпсму значению интегральной оценки / внутри области, назначаемой из других соображении.

Важно также иметь в виду, что выражение интегральной оценки через выбираемые параметры системы в буквенном виде может в ряде случаев оказаться сложным для исследования в общем виде. В таких случаях можно поступить иначе: задавать несколько числовых значений одного из выбираемых параметров (при жестко заданных всех остальных) и вычислять для каждого из них значения / (или /). В результате будет видно, при каких значениях данного параметра получается /, (можно для наглядности построить график величины / в зависимости от выбираемого пара.метра). Ана.тогично нужно поступить и с другими выбираемы.ми параметра.ми системы.

В конкретных расчетах всегда следует учитывать, что одновременно с таки.м выбором параметров нужно, во-первых, обеспечить хорошие статические свойства системы и, во-вторых, проследить, чтобы оптимальная точка пе оказалась сл1П1Псо.м близко!] к границе устойчивости, так как всегда надо и.меть некоторый запас устойчивости.

Рассмотрим в качестве нри.мера дифференциальное уравнение третьего порядка

(ooP + aiP + 2P + 3)/(0 = 4/(0. (8.77)

где i/(t) - входное задающее или возмущаюп1ее во.здействие. Пусть входное во.здействие \\i{t) = 1(f). Тогда изображение по Лапласу управляемой величины будет

Y(p) = --1.

Установившееся значение управляемой величины .здесь будет г/(оо) = С = Ьо/а-. Вычислим для этого случая интегральную оценку /. Так как и = 3, а m = О, то в соответствии с формулой (8.61) имеем

x4t =

2а;А

Далее но выражению (8.62) находим определитель

Д= О 2 - Р =йз( 1 2- Р з).

О -a-j а,