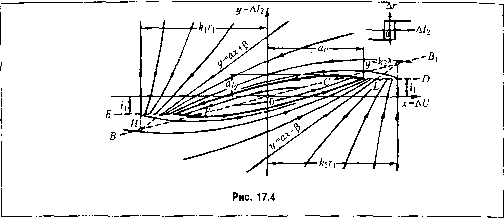где согласно (17.25), (17.26) и (17.28) и.меем

Аг = Г] sign(i/ - г,) при у < k2X,

Аг = г, sign(,z/ + z,) при у>к2Х\

(17.28)

(17.29)

следовательно, первое и,з этих условий имеет место ниже прямой ВВ,(рис. 17.4), а второе - выше нее. В первом слуте переключение реле происходит при у -г т. е. па прямой CD (рис. 17.4), а во втором случае - при у = -fj, т. е. па прямой £7*. Чертеж сделан в предположении, что ,21 i- результате получаем, что вьппе линии EFCD будет

Дг=г (17,.30)

а ниже линии EFCD

Ar = -r,. (17.31)

Рассмотрим сначала верхнюю область. Для нее, деля (17.28) па (17.27), с учетом (17.30) получим уравтгение фазовых траекторий

с1у 7 i у ~ кх dx Т2 x + k,t\

которое можно представить в виде

dy Т; у + 21 -k2{x + кг,) dx Т2 х + кг,

и проинтегрировать, применив вспомогательную подстановку

t/ + A,Vi=z(x+iri),

(17.32)

где 2 - новая пере.менная вместо у.

В результате найдем следуютее уравнение фазовых траекторий (при 7 , > Т.):

y-ax + + C{x + krУ (у> 1), (17.33)

где С] - произвольная постоянная,

(при Y = 1 решение будет и.меть другой вид, а при у < 1 будет а < О и (3 < 0; эти решения не будут исследоваться).

Чтобы представить себе всю совокупность фазовых траекторий, можно провести на фазовой плоскости прямую

=аг + 3 (17.35)

и ко всем ординатам этой прямой добавлять

У2 = С,(х + к,г,)у, (17..36)

придавая С, произвольные значения (каждому значению С, будет соответствовать определенная фазовая траектория). Это будут параболы степени у с осью

x=-kr (17.37)

и с единым пача.юм в точке Я (рис. 17.4), имеющей координаты

Ж=-,Г1, у-ккГу

На рис. 17.4 показаны все ветви этих парабол, лежащие выше линии EFCD (так как только там справедливы данные выкладки). Направления стрелок па полученных фазовых траекториях определяются тем, что проекция скорости изображаюп1ей точки dx

Чг справа от прямой (17.37) согласно (17.27) будет отрицательна, а слева -

положительна; проекция же -- согласно (17.28) вьпне прямой г/ = будет отрицательна, а ниже - положительна (во всех точках прямой у = j- касательные к фазовым траектория.м горизонтальны).

Аналогично строятся и все фазовые траектории ниже линии EFCD, так как их Дифференциа.льное уравнение отличается от (17.32) только за.меной на -г, согласно (17.31).

Б результате на рис. 17.4 видим, что все фазовые траектории, исходящие из особого отрезка FOC, расходятся, а все траектории, идущие от краев чертежа, сходятся. Как те, так и другие асимптотически приближаются к установивпюмуся предельному циклу, обозначенному на чертеже жирной замкнутой кривой (чичевицеобразной). Это соответствует тому, что установивишйся процесс в системе является автоколебательным, причем размеры предельного цикла а,; и й; иредставляют собой амплитуды автоколебаний соответственно напряжения At/и тока в обмотке магнита реле A/j-

Опрслелить фазовую траекторию, образуюн1ую .зтот преде;1ьнын цикл, можно как такую кривую (17.33), у которой

(17.38)

чем определяется значение произвольной постоянной С,. Зпачепиех(17.38) для этой

кривой и дает иско.мую амплитуду а. Амплитуда же а, определяется как ордината

пересечения кривой предельного цикла с прямой г/ = 2 (ибо, как было показано ранее, в точках .этой прямой касательные к фазовым траекториям ropnaoHTaJHjHbi).

Из чертежа (рис. 17,4) видно, что предельный цикл лежит левее точки Л и охватывает точку С. Поэтому Xq < йи < х т. е, амплитуда автоколебаний напряжения заключена в интервале

где а и Р определяются формулами (17.34); амплитуда же а будет немного больше г,.

Пример 5. Рассмотрим следящую систему с сухим трением в управляемом объекте, для которой уравнения были написаны в § 16.3. Уравнение обьекта (16.52) как нелинейного звена при отсутствии лиггейгюго трения (Сз = 0) имеет вид

ypP-rcsign 7)P = c,i при рО или рР = 0 иг >-, Р-const при рР = 0 ui\<-.

(17.39)

При написании уравнения линейной части системы (16.53) пренебрежем постояи-пыми врсмегп! (чтобы иметь возможность рассматривать уравпспие всей системы как уравнение второго порядка), а именно:

/, = -(оР+Л)р. Подставив это в уравнения объекта (17.39) и обозначив

-1 i

получим уравнение всей следящей системы в целом:

(р-1-fliP-I- з) Р =-1 sign рР при pPtO пли при рР = 0 иР>

Р = const прн ;)3 = 0 и!Р]<

(17.40)

(17.41) (17.42)