Jp(3 + C2p(3+csignp(3 = c]z при рО или рЗ = 0 и jzj, >-,

P = const при рР = 0 иг <-.

(16.53)

Уравнения всех остальных звеньев дашюй следящей системы в совокупности об-ра.зуют линейную 4acTii системы, единое уравнение которой для свободного движения упрощенно запишем в виде

(7> + l)z; = -[(Г р + \)k,p + k]. (16.53)

Следящая система с зазором. Предположим теперь, что в той же самой следя1цей системе нелинейность заключается не в сухом трении, а в наличии зазоров в силовой механической передаче между двигателе.м и управляемым объектом. Все эти зазоры объединим в один и изобразим его условно в виде вилки со свободным ходом ±Ь. Таки.м образом, между двигателем и управляемым объектом вклинивается теперь новое нелинейное звено, изображенное на рнс. 16.20, а, входную величину которого обозначим Р,.

Характеристика этого 1гелииейпого звеиа и.зображена па рис. 16.20, б. Смысл ее следующий. Если бы не было зазора, то 3 равнялось бы Р, и характеристикой была бы прямая под угло.м 45°, изображенная на рис. 16.20, б штрих-пунктиром. Вследствие шора при движении в сторону возрастания угла Р эта прямая сдвинется вправо на юличииу h (поводок при-к.мется к правой CTopoire !Илки). При изменении направления движения сначала поводок будет перемещаться внутри зазора, he двигая вилку (Р = const). На характеристике это соответствует горизонтатьному отрезку длиной 2Ь (АБ, или ЕГ,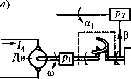

----- объект

Нелинейное звено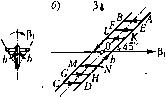

которого отрезка, а именно ири любом значении Мр \ < с. Этим определяется зона застоя системы. Застой проявляется в том, что, с одной стороны, система пе будет двигаться при изменении угла поворота командной оси в определенном интервале и, с другой стороны, что система будет обладать он1ибкой из-за сухого трения в положении равновесия. В процессе же движения системы в одну сторону с любой скоростью сухое трение внесет постоянную ошибку од1Юго знака, что соответствует как бы дополнительной внешней нагрузке М, . = с.

Итак, уравнение управляемого объекта, как нелинейного звена системы, соглас1го (16.48) и (16.49) с учетом (16.50) будет иметь вид

или KL, или другие в зависимости от фактического значения Р в зто время). Затем начнет дви1-аться и виЛка, что будет соответствовать прямой ВС, сдвинутой влево от начала координат на величину Ь.

Ири равновесии системы поводок и вилка .могут занимать ;iK)6oe относительное положение внутри зазора, что вызывает ошибку системы из-за зазора, равную ± Ь. 11ри движении системы в одну из сторон будет постоянное отставание объекта из-за зазора на величину ± Ь, не считая того отставания, которое будет enie из-за нагрузки.

Уравпение управляемого объекта, включавшее в себя и двигате.ть, теперь разобьется па два пелинейных. Первое нелииейиое уравпспие управляемого объекта с двигателем будет (ограничиваемся учетом одной постоянной времени)

(Г р + 1)/)р,=,г; при рРО, (7;р-г1)рр, =;,г;, при рр = 0

(16.5/1)

(соответственно с поводком, прижатым к вилке, и с поводком, свободно движущимся внутри зазора); Г, меньше Tq па величииуУц/сз, где/о - момент инерции управляемого объекта. Кроме этого, надо написать второе уравнение нелинейного звена с зазором, соответствующее характеристике рис. 16.20, б:

Р = Р,-й при рР, >0, р = р,-hfe при рР, <0, Р = const при]Р,-Р!<Ь.

(16.55)

Следовательно, управляемый объект будет иметь остановки при своих колебаниях, соответствующие участкам АВ, CD п т. д. характеристики рис. 16.20, б.

Линейная часть системы остается такой же, как в предыдущем примере, т. е. (16.53).

Система автоматической стабилизации давления (учет сухого трения). Рассмотри.м систему (рис. 6.27), уравнения которой в линейном виде были получены в § 6.7. В чувствительпо.м элементе 2 масса незначительна, но зато существенное значение может иметь сухое трение. Поэтому уравнение движения штока мембраны запишем в виде

р-г;,-7;.-7-, = о.

(16.56)

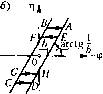где 7 - сила сухого трения, имеющая постоянную величину с, меия1011и1я направление ири изменении знака скорости рг/(рис. 16.21,а) и могущая принимать любые зиачеиия во время остановки, т. е.

F = с sign РУ ири РУ ф о, -c<7v <--с ири p.v = 0.

(16.57)

Р - сила давления воздуха камеры иа мембрану;/;, - упругая силамемб[)аиы;Гп -силапру-жииы.

isign рт] + 5г1 =-ф ири рг\0, или рг] = 0 и ;ф + 8г11>/;, Ti = const при ф + 5г1>.

(16.,э8)

где h =-; у - площадь мембраны; р - полпи1алы1ое давление в камере.

Построим характеристику :)Того нелииейиого.звенас сухи.м трением в координатах (-ф, Г). Легко видеть, что первое из уравнений (16.58) соответствует прямым DA и ВС при рт] > О и рг < О, а второе уравнение (т) = const) - отрезкам АВ, CD, EF, GH и т. п. на рис. 16.21, б. Из сравнения рис. 16.21, б и )ис. 16.20, б видно, что сухое трение в таком нелинейио.м звене (6e:i массы) эквивалентно зазору, ноловшта которого равна h, чего соверщетю нельзя сказать о сухо.м трении в следящей системе, где учи тывалась масса (.мо.мент инернии).

Все остальные зве1и>я системы образуют липейнзю часть, единое уравненпе которой при/ = О будет

(7>1)(7>+1)ф = ,Л. (16.59)

§ 16.4. Уравнения систем с нелинейностями других видов

dt О

d% dt

t А-Г

arctg

Рассмотри.м несколько примеров составления уравнений автоматических систем с иелииеЙ1гостями других видов, чем в §§ 16.2 и Кх.З.

Система автоматиче-с{сого управления с нелинейной характеристикой привода управляющего органа. 11)нвод управляю-1цего opiana, каким бы он ни был (электрический, гидравлический, пневматический), всегда имеет, во-нервых, некоторую зону нечувствительности в начале координат (рис. 16.22, а), и, во-вторых, зону насыщения . Кроме TOIO, может иметь место eiue и гистерезис (рис. 16.22, г). Эти две

arcLg kc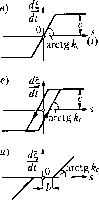

В результате после перехода к безразмерным относителыгым отклонениям (14.27) и (14.48) иолучи.м вместо (14.47) следующее уравнение чувствительного .элемента как нелинейногозвена: