Kpo.vic ограничений в виде неравенств используются также ограничения типа го-лономных связей

СДх ...,х ) = 0, (/г = 1,2,...,/), (24.7)

где Gfi - некоторая функция, а также ограничения тина пеголономпых связей в виде дифференциальных уравнений

C4(x,.....л ;д: ...;х ;...) = 0, ( = 1,2,...,/), (24.8)

изопериметрические ограничения в виде функционалов и др. [35].

Цель управления состоит в переводе объекта из начального состояния x(i(,) в некоторое конечное состояние х(с). Вид этих граничных условий определяется в соответствии с физическим смысло.м задачи, репше.мой системой автоматического управления. В одних случаях они задаются полностью:

х(?о) = о- x{tk) = x. (24.9)

Тогда имеем задачу с фиксированными или закреиленны.ми концами. В других случаях граничные условия (или одно из них) задаются лишь частично:

x{t)P, х{Ц)еР, (24.10)

где и - некоторые множества в пространстве состояний.

Момент окончания процесса может быть фиксировапны.м (заданным) или свободным.

Из всего множества возможных допустимых управлений пеобходи.мо выбрать такое, которое не только осугцествляет за/ганную цель управления, по и обеспечивает наилучшее значение выбранного показателя качества (быстродействия, расхода энергии и т. п.). Это .можно сделать, если сам показатель качества или критерий опти.маль-ности выражен в той или иной математической форме. Hanie всего он представляется в виде интеграла

I=jfo(x,u)dt, (24.11)

где /о - некоторая скатярная функция.

Выражение (24.11) называется функционалом, так как/зависит от выбора функции м (t) и получающейся при этом функции х (t).

Функционал (24.11) обычно конструируется так, чтобы ири оптимальном управлении его значение было мини.мальиым. Это всегда может быть сделано и в случае .максимума требуемого показателя качества.

В качестве иллюстрации рассмотри.м два конкретных примера.

Пусть система должна иметь максимальное быстродействие. Тогда, положив /о(х,м)= 1, получим: I = tii-t . Следовательно, необходимо пайти такое управление й (t), при котором tj-tQ= 7n,i . Значение tj не фиксируется. Минимальная длительность переходного процесса Гп,; даже для одного и того же объекта зависит как от граничных условий (24.9) или (24.10), так и от ограничений (24.5)-(24.8).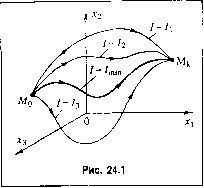

Пусть теперь управляемым объектом (24.3) является электрический двигатель, и - ток в его обмотке управления. R - сопротивление обмотки. Тогда при /(х,и) = Ки функционал (24.11) характеризует расход энергии на управление за промежуток времени - Iq. При .заданных граничных значениях (например, значениях угла и угловой скорости в моменты времени to и С.) и ограничениях па величину тока требуется найти такой закон изменения тока, при котором расход энергии окажется .мипимальпы.м. Дополнительное Офаничепие может быть наложено, например, па величину угловой скорости. Момент времени t обязательно должен быть ограничен (задан), так как в противпо.м случае оптимальным будет управление и = 0, при котором t =°° .

В общем случае функционал (24.11) может представлять любую желаемую комбинацию оценок ра.зличных качеств синтезируемой системы. Однако следует учитывать, что чем сложнее .этот функционал, тем труднее peniaeтся задача оптимизации даже для линейных одномерных объектов (24.3). Дополнительные трудности возникают при повышении порядка уравнений (24.1)-(24.3) и при наличии внешних воздействий,

С учетом изложенного задачу синтеза оптимального алгорит.ма управления .можно сформулировать следуюншм образом.

Пусть при п = 3 в трехмерном пространстве (рис. 24.1) начальному состоянию объекта соответствует точка Mq с координатами x{t(,), а конечному состоянию - точка Mf. с координатами х(С,).

Существует .множество допустимых управлений й (С), переводящих объект из начального состояния в конечное. Для каждого из них, решив дифференциальное уравнение объекта (24.1), можно найти траекторию х (t), азатем определить величину функционала (24.11). Из полученного множества управлений следует выбрать такое, при котором функционал принимает минима.,П)Ное значение. Это управление и будет оптимальным управлением, а соответствующая ему траектория - опти.мачьной траекторией.

Очевидно, что таким снособо.м решить задачу синтеза практически невозможно. Однако существуют другие способы оптимизации или, иначе говоря, методы синтеза оптима..1ЬПых систем, как аналитические, так и машинные. Все эти с1Юсобы в своей основе являются вариационными, но в отличие от предыдущего позволяют избежать перебора множества допустимых управлений. Каждый из них дает возможность довести решение задачи до К01ща в числовом виде. Для некоторых простейнтх задач удается получить аналитическое решение. Примером может служить рассмотренный в § 11.9 .метод синтеза линейной системы при случайных воздействиях по минимуму среднеквадратичной ошибки (задача Винера). В следующих параграфах будут в про-стейпю.м виде изложены основы некоторых других .методов синтеза. Кроме них следует отметить метод последовательной оптимизации на базе нелинейного нрогра.ммиро-вания, разработанный В. М. Пономаревым [77]. Важные направления развиты также в работах [26, 60, 67, 77] и других.

Получением оптимального алгоритма управления завершается ли1пь первый этан синтеза оптимальной структуры управляюп1его устройства. Па втором этапе требуется осуществить техническую реализацию алгоритма. Сложность решения этой задачи связана с тем, что при исполызовании большинства .методов синтеза оптимальный алгоритм получается в виде функции времени: u = u(t). При управлении по временной програ.мме система автоматического управления оказывается разомкнутой, так как она не контролирует фактическое состояР1ие объекта. Такой системе будут присущи все типичные для разомкнутых систем недостатки, о которых говорилось в главе 1.

Для построения за.мкнутой оптимальной системы управления м = й(С) необходи.мо каким-либо способо.м привести к виду (24.4), т. е. сфо1)мировать его как функцию переменных состояниях,-. В ряде случаев решение .этой .задачи ока.зывает ие .менее сложным, че.м синтез самого оптимального алгоритма. Но даже если оптимальное управление м = м(х) найдено, его можно реализовать лишь тогда, когда входящие в него переменные могут быть и; мереиы суп1ествующими техническими средствами (папри.мер, датчиками). Поэто.му часто прибегают к со.зданию пе строго оитй.мальных, а близких к оптимальным систем. Некоторые конкретные рекомендации по таким системам даны в работе [44J.

§ 24.2. Использование классических вариационных методов

Методы классического вариационного исчисления были ра.зработаны ешс в XVni векеи ие предназначались для синте.за оптимального управления объектом. Рассмотрим одну из классических задач. Пусть задан функционал

I = jfo(x ...,x ;Xi,..,.x )dl, (24.12)

гдех,- - некоторые дважды дифференцируемые функции, среди которых необходи.мо иайти такие функции Xj(t) или экстремали, которые удовлетворяют заданным граничным условиям Xjit), х,-(г:,() и минимизируют фупкциопа-ч (24.12), Экстремали от ыскиваются среди решепий уравнений Эйлера

Эх,- dt

Эх,-,

= 0, г = 1,2,..., п. (24.13)

Для установления факта мипи.мизации функционала необходимо удостовериться, что вдоль экстремалей выполняются условия Лагранжа

Эх,?

2 >0, г = 1,2...., и, (24.14)

аналогичные требованию положительности второй производной в точке мипи.мума функции.