За координаты фазовой плоскости примем, как обычно, X = р, = рр. Условие 11 = 0 и I I

при котором согласно (17.42) будет Р = const, т. е.

система будет в равновесии,

изображается па фазовой плос-кост и отрез кохг /1В (р и с. 17.5).

Вне этого отрезка согласно (17.41) необходимо отдельно

рассмотреть два случая: i/ = рР О и г/ = рР < О, т. е. Bcpxtnoio и нижнюю половины фазовой нлоскости. При г/ < О и.з (17.41) имеем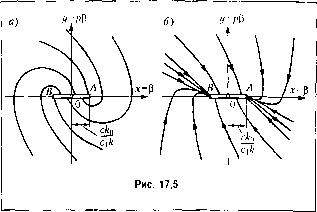

(j/ + а,р + (i.j)x = Ь,

(17.43)

1

Это уравненпе совпадает с уравнением (16.23), но со сдвигом на величину ~

Следовательно, ниже осп х надо нанести такие же кривые, как на рис. 16.9, б (если flj < 42) или как на рис. 16.11, б (если я, > 4а2), но со сдвигом начала координат в точку Л, что и сделано на рис. 17.5, аиб соответственно.

Апатогичные кривые наносятся и выше оси х, по только со сдвиго.м иачача координат в точку В (рис. 17.5), так как согласно (17.41) при г/ > О имеем уравнение

(p + ap + a2)x=-h. (17.44)

В обоих случаях (рис. 17.5, а и б) систе.ма устойчива, причем в перво.м случае переходный нроцесс состоит из конечного чиста затухающих колебаний, а во втором случае и.меем.апериодическое движение. Положение равновесия объекта определяется неоднозначно, он может остановиться в любой точке особого отрезка АВ (рис. 17.5), Как это было уже ранее при наличии зоны нечувствительности (см. пример 1). Особый отрезок ЛВ определяется соотношением ] М ! = \ci \ < с, где с - абсолютное значение .момента сухого трения при движении управляемого объекта.

За.меги.м, что произведенное здесь упрощение уравнений системы хотя и позволило репшть их точно, но это решение, дающее в результате устойчивость систе.мы при любых числовых значениях пара.метров систе.мы, неполно отражает действительную картину явлений в данной нелинейной систе.ме.

§ 17.2. Теоремы прямого метода Ляпунова и их применение

Предварительно за.мети.м, что при и.зложеиии прямого метода Ляпунова, и.менуе-мого также второй методой Ляпунова, будем пользоваться дифференциальными уравнениями автоматической систе.мы в форме уравнений первого порядка, или уравне-

НИИ состояния, полагая, что они записаны для переходного процесса в отклонениях всех переменных от их значений в установившемся процессе при щщых постоянных значениях возмуп1ающего/ = /* и задак)П1его g = g° воздействий. Следовательно, .зти уравнения для нелинейной системы и-го порядка будут:

dt dx ~dt

-X,(Xi,X2,.,.,X ), = Х2(.Г Ж2,. ,Х ),

(17.45)

-~- = X (X X2,...,X ),

где функции X, X2, ., X произвольны и содержат любого вида нелинейности, но всегда удовлетворяют условию

X, =Х2 = ... = Х = 0 при ж, =X2-...=x = 0, (17.46)

так как в установившемся состоянии все отклонения переменных и их производные равны, очевидно, нулю но само.му определению понятия этих отклонений. Нам понадобятся в дальнейшем еще следующие сведения.

Понятие о знакоопределенных, знакопостоянных и знакопеременных функциях. Пусть имеется функция нескольких переменных

V= V(x X2.....х ).

Представим себеи-мерное фазовое пространство (см. § 16.1), в которо.м л- зГ2,..., х являются пря.моугольными координатами (это будут, в частности, фазовая плоскость при и = 2 и обычное трех-мерпое пространство при п = 3). Тогда в каждой точке указанного пространства функция Убудет иметь некоторое определенное значение. Нам понадобятся в дальнейшем функции V(xi,X2,..., х ), которые обращаются в пуль в начале координат (т. е. при = л2 = ... = зг = 0) и непрерывны в некоторой области вокруг пего.

Функция Vназывается знакоопределенной в некоторой области, если она во всех точках этой области вокруг начала координат сохраняет один и тот же знак и нигде не обрапщется в нуль, кроме только са.мого начала координат.

Функция Vназывается знакопостоянной, если она сохратгяет один и тот же знак, но может обращаться в нуль не только в начале координат, но и в других точках данной области.

Функция Vназывается знакопеременной, если она в датиюй области вокруг начала координат .может иметь разные знаки.

Приведем при.меры всех трех типов функций У. Пусть и = 2иУ = х +Х2- Это будет знакоопределенная (положительная) функция, так как У = О только тогда, когда одновременно ЗГ, = О hx2 = О, и У> О при всех вещественных значениях д,-, h.Tj. Аналогично при любом и функция V = х\ +х1+...х1 будет зиакоопределепной положительной, а У = -(xf -ь х -ь.. .х,) - знакоопределенной отрицательной.

Рис. 17.9

Если взять функцию У-х\л-х\ при п = З.тоопауже не будет знакоопрсделенной, так как, оставаясь ноложитетьной при любых Х\, Х2 И Хз она может обращаться в нуль не только при Xi = Хз = Хз = о, но также и при любом значении Хд, если х, = Хз = О (т. е. на всей ocH.Xj, рис. 17.9, а). Следовательно, это будет знакопостоянная (положительная) функция.

Наконец, функция V = х, + Хз будет знакопеременной, так как oira положительна для всех точек плоскости справа от прямойх! = -Xj (рис. 17.9, б) и отрицательна слева от этой прямой.

Заметим, что в некоторых частных задачах нам понадобится также функция V, которая обращается в нуль не в начале координат, а на заданном конечном отрезке ЛВ (рис. 17.9, в). Тогда зпакоопределетюсть функции Кбудет обозначать ее неизменный знак и необращение в нуль в некоторой области вокруг этого отрезка.

Функция Ляпунова и ее производная по времени. Любую функцию

1/=1/(Х Х2,..., Х ),

(17.47)

тождественно обращающуюся в нуль нрих, =х2 = ... = х = О, будем называть функцией Ляпунова, если в ней в качестве величинх ...,х взяты те отклонения пере.менных в переходном ироцессе

X, = X, (t), Хз = Хз (О,х = х (О,

в которых записываются уравнения (17.4.5) для этой системы. Производная от функции Ляпунова (17.47) по времени будет

dV dV dx, dV dx

dt Эх, dt Эхз dt

dx, dx,

2 dV dx

Эх dt

(17.48)

й(Х й(х

Подставив сюда значения заданных уравнений систе.ма в общем

случае (17.45), получим производную от функции Ляпунова по временив виде

гдеХр Х2,..., Х - правые части уравнений (17.45), представляющие собой заданные функции от отклонений Х Х2,. . .,х .

Следовательно, производная от функции Ляпунова по времени, так же каки сама У, является некоторой функцией отклонений, т. е.

= W/(X X2,...,X ),

(17..50)