лд-,

2+ hp

. , 2 2 .3 3

Рис. 3.4

p = d/dl или ко.мплекспую величину рс+ ]ш в зависимости от того, рассматриваются ли функции времени пли их изображения.

Понятие передаточной фу1п<ции весьма удобно при анализе так пазывае.чплх структурных схем. Так, например, звено, изоб1)ажепное на рис. 3.1, после линеаризации, которая была проделана в предыдущем параграфе, .можно представить в виде структурной схемы, показанной па рис. 3.4. Передаточные фу1п<ции звеньев или отде.тьных участков схемы позволяют легко получить общее уравнение всей системы в виде (3.13) или (3.20), а в дальнейшем в случае необходимости перейти к исходному диф())еренциальиому уравнению вида (3.9). Подобным же образом могут быть получены передаточ1И>1е функции и структурные схемы и для других диф-ферепциьчьных уравнений звеньев, например для рассмотренного выше уравнения (3.10). Подробнее :-)Тот воп[юс изложен в § 5.3.

Глава 4

ДИНАМИЧЕСКИЕ ЗВЕНЬЯ И ИХ ХАРАКТЕРИСТИКИ

§ 4.1. Общие понятия

Как уже было сказано, для расчета различных систем автоматического управле-иия они обычно разбиваются на динамические звенья. Под дина.мическим звено.м понимают устройство любой физической природы и конструктивного оформления, по описываемое онределенны.м дифференциальным уравнением,

Классификация звеньев производится именно но виду дифференциального уравнения. Одним и тем же уравнением могут описываться весьма разнообразные устройства (механические, гидравлические, электрические и т. д.). Для теории автоматического управления это будет один и тот же тин звена. Конкретные же элементы авто.матических систем, их теория, конструкция и расчеты излагаются в соответствующих учебниках и руководствах.

Обозначим входную величину звена через г а выходную через .Tj (рис 4.1). Возмущение, действующее на звено, в соответствии с изложенны.м выше обозначим/(£), Статическая характеристика любого звена может быть изображена прямой линией (рис. 4.2), так как пока будут рассматриваться линейные или, точнее, линеаризованные

CHCTCXHjI.

в звеньях позиционного, или статического, типа линейной зависн.мостью л2 -i связаны выходная и входная величины в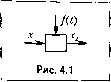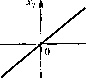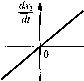

Рис. 4.2

установившемся режиме (рис. 4.2, я). Коэффициент иропорциональиости к .между выходной и входной величинами представляет собой коэффициент передачи звена.

В звеньях интегрирующего типа линейной зависи.мостыо Jxj/A = кх связаны производная выходной величины и входная величина в установившемся режиме (рис. 4.2, б). В этом случае для установившегося режима будет спрапедл1ИП)1м равенство Х2 = к xdc, откуда и произошло название этого типа звеньев. Коэффициент пропорциональности к в этом случае также является коэ(})фициентом передачи звена. Если входная и выходная величины звена имеют одинаковую размерность, то коэф(})нциеиту передачи соответствует раз.мерпость [с

В звеньях дифференцирующего типа Л1Н1ейиой зависимостью Х2 = к dx/dt связа-iH)i вустановивп1емся режи.ме выходная величина и производная входной (рис. 4.2. в), откуда и произошло название этого типа звеньев. Коэффициент пронорциональнос-ти к является коэффициентом передачи звена. Ecjhi входная и выходная величины и.меют одинаковую размерность, то коэффициенту передачи в это.м случае соответствует размерность [с].

Классификация звеньев, как уже отмечалось, производится ио виду дифференциального уравнения или, что то же самое, по виду передаточной функции звена. Предиоложи.м, что звено, изображенное на рис. 4.1, описывается лифферспциаль-пым уравнением, представленным в стандартной форме:

Г., + Т, + Х2=к,Х,+к2

dx-,

dx, dt

При нулевых пача.-и>пых условиях, т. е. в том случае, если для г < О входная и выходная величины, а также их производные тождественно равны нулю, и при отсутствии внешнего возмущения (/{t) = 0) может быть найдена передаточная функция звена как отношение изображений по Лапласу выходной и входной величин:

Х,{р) \ + 1]р + т1р 1 + 1\р + Т!р

(4.1)

где к, - коэффициент передачи звена, Т- = jAi ~ постоянная времени.

При известной передаточной функции выходная величина (точнее, ее и.зобра-жение по Лапласу) может находиться из выражения

§ 4.2. Временные характеристики

Динамические свойства звена могут быть определены но его переходной функции и функции веса.

Переходная функция, или переходная характеристика, h{C) описывает переходный процесс на выходе звена, возникающий при подаче на его вход скачкообразного воздействия при величине скачка, равной единице (рис. 4.3). Такое входное воздействие называется единичной ступенчатой функцией и обозначается x{t) = \{t), что соответствует х, = О при С < О и Х; = 1 при t> Предполагается, что единица имеет ту же размерность, что и физическая величина на входе звена.

Если входное воздействие представляет собой неединичную ступенчатую функцию х, = N \{t), выходная величина будет равнах2 = Nh{t).

Ступенчатая функция представляет собой распространенный вид входного воздействия в автоматических системах. К такому виду сводятся мгновенное изменение нагрузки электрического генератора, мгновенное возрастание нагрузки на валу двигателя, мгновенный поворот командной оси следяп1ей системы и т. п.

Умножение какой-либо функции времени x{t) па единичную ступенчатую функцию \{t) означает, что функция времени х(0 будет суп1ествовать только при t > О, при ? < О она обращается в нуль. Это иллюстрируется рис. 4.4.

Функция веса w{i) представляет собой реакцию звена на единичную импульсную функцию, поданную на его вход (рис. 4.5).

Ана,.!огичным образом может быть найдена передаточная функция звена по возмущению, если положить при пулевых начальных условиях входное воздействие равным нулю (х, = 0). Тогда искомая передаточная функция будет равна отношению изображений выходной величины и ннепгнего возмущения:

в дальнейшем изложении для характеристики звена будет использоваться в основном передаточная функция, так как именно она дает связь между входной и выходной величинами, что необходимо знать при использовании того или иного звена в автоматической системе.

В соответствии с этим в табл. 4.1 приведены передаточные функции десяти разновидностей так называемых типовых диггамических звеньев. Под типовым звеном понимается такое звено, которое описывается дифференциальным уравнением не выше второго порядка. Характеристики типовых звеньев рассматриваются более подробно ниже.

В табл. 4.1 не приводятся сведения о большой группе так называемых корректирующих звеньев, используемых для улучшения динамических качеств автоматических систем. Эти звенья будут рассмотрены в главе 10.