При исиользовании преобразования z е частотная передаточная фурп<ция W{e) является транспепдентиой. Поэтому для систем выше второго порядка построение а. ф. X. существенно затрудняется. Кроме того, практически исключается возможность построения асимптотических логарифмических частотных характеристик.

Для преодоления указанных недостатков удобно использовать преобразование

2 =-f. (14.99)

Оно, как и иреобразовапие (14.90), является билинейным и отображает круг единичного радиуса с плоскости z на левую полуплоскость плоскости переменной X, что дает возможность применять все критерии устойчивости пснрерыв1нях систе.м.

Переменная X называется абсолютной исевдочастотой, или сокращенно - псевдочастотой. Сравнив (14.99) с (14.97) получим:

Х = -Щ-. (14.100)

Г 2

Из (14.100) видно, что благодаря со.множителю 2/Гпсевдочастота X имеет раз.мерность угловой частоты. Кроме того, ири изменении частоты w от О до л/7она из.меняется от О до оо. Наконец, при w < 2/Гпсевдочастота практически совпадает с реальноГ! частотой (О.

При исследовании устойчивости и качества и.мпульсных систем можно оперировать с jX точно так же, как это делалось cju) или с р при исследовании непрерывных систем.

В качестве примера используем подстановку (14.99) в передаточной функции (! 4.97). В результате получим частотную передаточную функцию разомкнутой системы

W{jX)--. (14.101)

Теперь для исследования устойчивости замкнутой системы .можно применять как алгебраический критерий, так и критерий Найквиста.

В первом случае находи.м ха1)актсристическое уравнение .за.мкнутой системы:

]Х + К=0.

Необходимое условие выполняется при КТ< 2. Для системы nejBoro порядка оно является и достаточным.

Во вто[)ом случае находим модуль и фазу:

KJ\ + X -

WiJX)

V() = -90°-arctg.

Нетрудно убедиться, что а. ф. х. разомкнуто системы будет точно такой же, как на рис. 14.9, а, только она закончится иа оси a6cinicc при Х = оо.

На рис. 14.9, б и.зображены логарифмические частотные характеристики разомкнутой систе.мы. Так как в знаменателе (14.101) имеетсяjX, что эквивалентно наличию р в знаменателе иередаточной функции ненрерывиой системы W(p), то первая асимптота имеет наклон -20 дБ/дек и пересекает ось абсцисс при X = К. На сопрягающей частоте X = 2/Гл.а.х. изла.мывается па -20 дБ/дек, так как со.\П10житель 1 - jXT/2 находится в числителе. Если К<2/Т, то вторая аси.мптота проходит ниже оси абсцисс. При этом критический от])езок находится левее точки Х = Км логариф.мическая фазовая характеристика пе пересекает eio. Следоватольно, замкнутая система устойчива. Если же К > 2/7, то вторая аси.мптота проходит выше оси абсцисс и критическим отрезком будет вся эта ось. Прн ?i = оофа.за VjJ (w) = -180 , а модуль не равен бесконечности. Следовательно, имеет место -1 /2 перехода н замкнутая система неустойчива.

§ 14.7. Оценка качества импульсных систем

Обише соображения по оценке качества систем автоматического уиравлегщя, рассмотренные в § 8.1, относятся и к и.мпульсным система.м.

Для оценки точности можно использовать величину опшбки в типовых режимах. В первых трех из них (см. § 8.2) при отсутствии воз.мупения значение установившейся оишбки в любой мо.мент времени в соответствии с теоремой о конечном значении (14.37) определяется но (1)ормуле

х .г(е) = limx(/,e) = lim(2 - 1)Х(2,е), (14,102)

X(2,t:) = G(2,e)- У(2,е),

G(2, е) = Z{g{t)) - изображепие задающего 1зо;злсйствия, а К(2, е) определяется выражением (14.77).

В дискретные момеггты времени= П

х ,=Мщ(2-1)Х(2), (14.103)

где X{z) определяется выражением (14.65).

Следует отметить, что необходи.мость в использовании формул (14.102) или (14.10.3) возникает только тогда, когда скважност ь импульсов на выходе формирующего устройства системы (рис. 14.7) Y< 1.11сли7= 1, то в установившемся состоянии сигнал на выходе этого устройст1зал-* будет постоянным и и\н1ульспая систе.ма .может рассматриваться как непрерывная. В этом случае для оценки точности, в том числе и возмупиющих воздействий, можно пользоваться формула.ми, приведет1ыми в § 8.2.

В режиме движения ио гармоническому закону (8.12) частота 0),обычно сравнительно мала, HpH4e.vr всегда а), < 2/Г. При это.м условии псевдочастота в соответствии с (14.100) практически совпадает с реальной частотой 0), и для расчетов можно использовать формулы (8.15) и (8.16), положив в inix W(j(i>) = MoO )-

Установившаяся точность импульсной систе.мы может оце1н1ваться и но коэффи-циегггам 01пибок. Аналогично непрерывным системам, начиная с некоторого момента вре.мени ошибку можно представить i! виде ряда

x(j) = Cog{i) + cg(i) + g(i) + ...,

(14.104)

1де коэффициенты ошибок С( с Cj,... представляют собой коэффигщепты разложения нередаточной функции но ошибке Фд.(2) при 2 = е в ряд Маклорена по степенямр, т. е.

(14.105)

J/)=0

Оценка качества HNUiyjibcnott системы может делаться ностроитем кривой пе])е-ходного процесса, что при использовании 2-иреобразования осуп1ествляется сравин-тельно легко (§ 14.2).

Максималыюе згшчепие 1юс.;1едователыюсти может ие совпадать с максима.-ть-1П>1М значением переходной характеристики (рис. 14.10, а). Обычно это несовпадение не имеет существшнюго значения для определения за1шса устойчивости chctcnHjI. 0,ч-нако в отдельных случаях оно .может быть суп[ественным (рнс. 14.5, б). Чаще Bceio .это бывает при наличии в знаменателе передаточной функции непрерывной части системы Wq(p) сомножителей с комплексными корнями типа Тр +2L,J.p+ \. Можно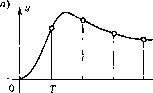

27 Ж 4 г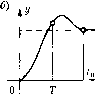

TV ЗГ 4Г