Для характеристики полезных входных сигналов систем уп])авлепия соотношения (11.39) и (11.40) практически не могут применяться, так как для зтих сигналов ход процесса в последующие мо.менты времени в какой-то степени зависит от того, что было в предыдущие моменты времени.

Так, например, если речь идет о слежении за самолетом, то он пе может- как угодно быстро .менять свое положение и скорость. Поэтому если он в .момент времени г, занял иоложение х то этим самым его возможное положение Х2 в следуюпцш момент 2 ограничено, г. е. события (х2, 2) и (х Z.,) не будут независимыми. Че.м более инерционен изучаемый объект, тем больше эта взаимозависи.мость, или кор[)еляция. В таких случаях вместо фор.мулы (11.39) необходи.мо записать

W2{X,tx\X2,t2)AXvh)-l.\{4-l\ . (И.41)

где W21 (х2, 2)fi?r- условная вероятность того, что случайный процесс пройдет вблизи точки (Х2, t, если он уже прошел через точку (х f,).

Следовательно, зная плотности вероятности ш (х и (Xj, t(, Xj, /-2), .можно найти также и условную плотность вероятности

W2l(X2,t2)------. (11.42)

HXi,ti)

Кроме того, имеет место следующая связь между основными плотностями вероятности:

W{Xi,ti)= Ш2(Х[,[;.Г2,2У-2 (11.43)

так как Z0 (х Г,) есть плотность вероятности случайной величины (х Г,) безотноси-те.чьно к тому, какое йотом будет значение (х2, 2), т. е. допускается < Х2 < +°°. Аначогичным образо.м любая плотность вероятности низшего порядка всегда может быть получена из высшей, т. е. высише плотности вероятностей содержат наибольшее количество инфор.мации о случайном процессе (о взаи.мосвязях между возможными значениями случайной величины х в ра.зличные моменты времени).

Написанные соотношения справедливы для случайшлх процессов любых типов. В зависимости же от того, до какого порядка принимаются во внимание плотности вероятности, а также от разных дополнительных гипотез о формах связи между w, №2,рассматриваются разные типы случайных процессов в от;н1Чие от чисто случайных.

Другая классификация всех случайных процессов состоит в ])а,зделении их на стациопарпые и нестационарные. Теория стационарных случайных процессов наиболее разработана и чаще всего применяется на практике.

§11.3. Стационарные случайные процессы

Стационарным случайным процессом называется такой процесс, вероятностные характеристики которого не зависят от вре.мени. Все плотности вероятностей ж W2,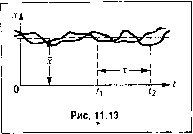

не меняются при любом сдвиге рассматриваемого участка процесса во времени, т. е. при сохранении ностоящюй разности.

Можно ска.зать, что стационарный с;лучайиый процесс в какой-то мере анатогичен обычным стационарным или установив и 1и.МСЯ процессам в автоматических систе.мах. Напри.мер, при рассмотрении обычных установившихся периодических колебаний ничего не изменится, если перенести начало отсчета на какую-нибудь величину. При этом сохранят свои значения такие характеристики, как частота, амплитуда, среднеквадратичное значение и т. н.

В стационарном случайном пропессе закон распределения один и тот же для каждого момента времени, т. е. плотность вероятности не зависит от вре.мени: w (х, t) = w (х).

Отсюда иолучае.м х = const и а = const вдоль всего случайного процесса. Следовательно, в стационарном случайном процессе средняя линия, в отличие от общего случая (см. рис. 11.12), будет пря.мая х = const (рис. 11.13), подобно постоянному смещению средней линии обычных периодических колебаний. Рассеяние значений переменной х в стационарном случайном процессе, определяемое а = const, также будет все время одинаковым, подобно постоянному значению среднеквадратичного отклонения обычных установившихся колебаний от средней линии.

Апатогичным образом и двумерная плотность вероятности также будет одна и та же для одного и того же промежутка времени 1 = 2 i между ;нобымн и 2 (рис. 11.13), т е.

W2 (х С,; Х2, 2) = W2 (X Х2, t), (11.44)

и также для -мерной плотности вероятное .

Задание всех .этих функций распределения плопюсти определяет случайный процесс. Однако более удобно и.меть дело с некоторы.ми осредненными и харакТеристи-ка.ми процесса.

Прежде че.м перейти к ним, отметим два важных для практики свойства.

1. Ограничиваясь только стационарнььми случайны.ми npoiieccaMH, можно будет определить только установившиеся (стационарные) динамические ошибки авто.матических систе.м при случайных воздействиях. Такой прие.м применялся и ранее при рассмотрении регулярных во.здействии, когда определялись динамические свойства систем по величине динамических оигибок в установившемся периодическо.м режиме.

2. Стационарные случайные процессы обладают замечательным свойством, которое известно под названием эргодической гипотезы.

Для стационарного случайного процесса с вероятностью, равной единице (т. е. практически достоверно), всякое среднее по .множеству равно соответствуюн1ему ереднему по времени, в частности f = х, х = х и т. д.

В са.мом деле, поскольку вероятностные характе])истики стационарного случайного процесса с течением вре.мени не меняются (например, х = const), то длительное наблюдение случайного процесса па одном объекте (среднее по времени) дает в среднем такую же картину, как и болыпое число наблюдений, сделанное в один и тот же момент вре.мени на больпюм числе одинаковых объектов (среднее по .множеству).

xw(x)dxxVm x(t)dt. (11.45)

2г ,

Аналогичным образом могут быть записаны .мо.менты более высоких порядков -дисперсия, среднеквадратичное отклонение и т. п.

Эргодическая гипотеза позволяет сильно упроп[ать все расчеты и эксперименты. Она позволяет для определения i , D, о и т. п. пользоваться одной кривой х (t), полученной при испытании однот ! систе.мы в течение длительного времени вместо параллельного испытания многих однотипных систе.м в один и тот же мо.мент времешт

Таким образо.м, важное свойство стационарного случайного процесса состоит в то.м, что отдельная его реализация на бескопечпо.м про.межутке времени полностью определяет собой весь случайный процесс со всеми бесчисленными возможгилми его реализациями. Этим свойством не обладает никакой другой тип слу1гайиого процесса.

§11.4. Корреляционная функция

Началын>1Й корреляционный момент двух значений случайной функции х(1.) и x{ti), В.ЗЯТЫХ в мо.менты вре.мени и г, носит название корреляционной (автокорреляционной) функции. Она .может быть найдена аналогично (11.31) из выражения

R(t,ti) = M[x(t)x(t)\= J jx(t)x(l)ze.2ix,t,x t)dxd.x. (11,46)

где вместо параллельного испытания многих однотипных систем в один и тот же момент времени w2 (х f,; х2, 2) двумерная нлот110сть вероятности.

Иногда под корреляционной функцией понимают центральный корреляционный моментx(i) nx(t), т. е,

R\t,t,) = M\{x(t)-m}{Ht,)~-4h)}\= j jlx(t)-x(t)mt)-

(11.47)

-x{t )]w2{x,t;x ) dxdx.

В этом случае корреляционная функция (11.46) может быть представлена в виде суммы

Rit,t) = x(t)x{h) + R4t,t,). (11.48)

Корреляционная функция является весьма универсальной характеристикой для случайного процесса. Она определяет зависимость случайной величины в последующий .момент времени х (t,) от предпюствующего значения x(t) в момент времени Это есть мера связи между ними.

Цля многих случаев сун,ествует математическое доказательство этого свойства. Тогда оно сводится к эргодической теореме.

Итак, среднее значение (математическое ожила)1ие) для стационарного процесса будет

х= -