4. Колебательное звено. Звено опись[вается тем же дифференциа.чьиым уравнением (4.25), что и апериодическое звено второго порядка. Однако корни характеристического уравнения 7+ iP +1=0 должны быть комплексными, что будет выполняться при 7i < 2Г1

Левая часть диффере1П1иального уравнения обычно представляется в виде

(TV2t;Tp+l)x,-kx,

X2=kx

(4.,31)

(4.32)

где q = 1/Т - угловая частота свободных колеба[шй (при отсутствии затухания), а С, - параметр затухания, лежап[ий в пределах Q<C,<i. Передаточная функция колебательного звена

2 2

1 + 2С7> + 7->

1-ь-=- + -- -

(4.33)

Примеры колебательных звеньев приведены на рис. 4.14. К ии.м 0Т1юсятся коле-бателыпяе 7?1С-цепи (рис. 4.14, а), управляемые двигатели иостояшюго тока при выполнении условия 47я > 7м (рнс. 4.14, б), упругие механические пе)едачи, напри.мер для передачи вра1цательного движения (рис. 4.14, в), с упругостью С, .мо.ментом инерции J и коэффициентом скоростного трения S, гироскопические элементы (рис. 4.14, г) и др.

Рассмотрим для иллюстрации гироскопический элемент (рис. 4.14, г). В качестве входной величины примем момент М, прикладываемый к оси а, а в качестве выходной - угол поворота этой же оси.

Уравнение равновесия моментов на оси

.da й?а .,d dr dt dt

Будем считать, что на оси 3 (оси прецессии) не действуют никакие внешние мо.меиты. Тогда для этой оси уравнение равновесия моментов за[инцстся так:

Л,Я = 0.

В этих формулах Л и 7? - моменты инерции относительно осей аир, - кинетический .мо-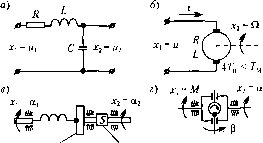

Маховик Демпфер Рис. 4.14

(АВ 2 fB ,

Это уравнение можно переписать следующим образом:

q q

0 0 I f [в

где q = H /АВ - квадрат угловой частоты нутационных колебаний, а s = JJv ~~

параметр затухания, определяемый действием сил скоростного Т1)ения на оси а. Это ypaBHCiHie совпадает с вь[ражением (4.32).

Для ре[[1ения диффepe[щиaJH,нoгo уравнения (4.31) или (4.32) необходимо найти корпи характеристического уравнения

7V+2C7p-fl = + -fl = 0.

Решение дает

р, 2 = -У ± Д = ±;>/ГЧ = <q±jq. (4.34)

Вещественная часть ко]шя у представляет собой коэффициент затухания переходного процесса, а л - частоту затухающих колебаний.

Временные характеристики зве[[а [[рнведены в табл. 4.2, а частот[1ые характеристики - в табл. 4.3.

А.мнлитудно-частотпая характеристика .может иметь резонаноняй ник. Исследование модуля частотной передаточной функции на максимум показывает, что пик будет существовать при < 0,707. Высота пика будет тем боль[[[е, чем меньше параметр затухания:

Макси.муму а, ч. х. соответствует частота

(Om=Wi-2C. (4-36)

мент гироскопа, равный его [юлярпому моменту инер[щи J, умноженному на угловую скорость собстве[[[[ого вра1це[[ия Q и F - ко:)ффицие[[т скоростного сонротив- ления на оси а.

Переходя к операто1)[н>[М выражениям и рёпгая оба уравнения совмест[10, получаем:

Л. а. x. строится ио выражению i(a)) = 201g-

2 n2

(4.37)

Однако построение л. а. х. не может быть сделано так просто, как это было для предыдущих звеньев. Для построения используются так называемые нормированные л. а. x. Постоянный множитель под знаком логарифма в выражении (4.37) может быть выделен в отдельное слагае.мое:

Z.(co) = 20lg/ + 201g-

+ 4С,

2 (Л

(4.38)

Построение первого слагаемого (4.38) не представляет никакого труда. Второе слагаемое может быть построено в функции относительной частоты (n/q для ра.злич-ных значений параметра затухания в виде уггиверсальных (нормированных) кривых (рис. 4.15). Для построения истинной л. а. х. необходимо выбрать нормированную л. а. x., соответствующую данному значению С поднять ее параллельно самой себе на 20 Ig и по оси частот от относительной частоты перейти к действительной умножением на q.

В функции той же относительной частоты на рис. 4.15 паиесепы нор.мироваиные л. ф. x., построенные по выражению

\/ = -arctg

2

(4.39)

Построение л. а. х. колебательного звена .можно делать также посредство.м проведения двух асимптот с наклона.ми О и -40 дБ/дек, иересекаюпцгхся в точке со = \/q, с последующим введеиие.м поправки, которая приведеиа на рис. 4.16.

Нормированные переходные характеристики колебательного звена для случая k = 1 приведены на рис. 4.17 в функции относительного времени qt.

Сравнение рис. 4.15 и 4.17 показывает, что снижение параметра .затухания t, приводит к повышению колебательности переходного процесса и росту резонансного пика амплитудной частотной характеристики.

5. Консервативное звено. Консервативное звено является частным случаем колебательного при = 0. Тогда передаточная функция (4.33) будет иметь вид

W{p)-.

(4.40)