9(а,со) =

(18.156)

-CO.

(18.157)

Эти два уравнения с дву.мя неизвестными а и со решаются графически. Для этого по формулам (18.154) с учетом (18,151) и (18.152) строятся грас})ики q (со) и q (со) при разных значениях а = flj, а, а,... (рис. 18.31, а). Зате.м на первом из них наносится кривая 1, определяемая правой частью уравнения (18.156), а на втором - кривая (18.157). Решение определится точками пересечения, для которых значения а = а и со = СОп одинаковы на обоих графиках. Найденные значения а и со будут ис-комымрг амплитудой и частотой автоколебаний,оп-ределяе.мых приближенно в видех = а sin сОп t. Полученные конкретные чис/ю-

соответствуют все.м заданны.м пара.метрам объекта и системы упраштения. Если изменить параметры систе.мы, из.менятся также з,.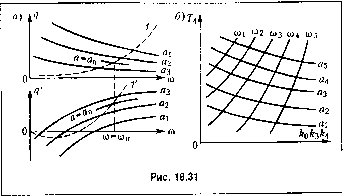

Найденные значения ди q согласно (18.151) и (18.152) являются вполне определенными функциями искомых величин а и со (амплитуды и частоты автоколебаний !!ереме1Н10Йх).

Характеристическое уравнение рассматриваемой систе.мы в целом после указанной гармонической линеаризации нелинейности, согласно (16.66)-( 16.69) и (18.153), принп.маетвид

Т,Т,Т + (TJ, + ГоГ, + ГзГ,)+ (Го + 7з + Г, )р+р + к,кф, р +

+ кокзкд(а,т) = 0. (18.155)

Для отыскания синусоидального периодического решения подставляем р =joi. Нолучае.м вещественную и мнимую части соответственно

X = kok q (а, со) - (Го + Тз + 71 + со = 0;

У = кдккд (а, со) + со - (TJ. + TJ + Г3Г4) со = 0.

Отсюда

и 0). На том же графике можно п[)Оследить влияние изменения параметров системы, для чего нужно менять коэффиииенты правых частей (18.156) и (18.157) при построении пунктирных кривых 1, 1 нарис. 18.31,а.

Изложенное выше решение удобно, если все параметры системы заданы. /1ля изучения же зависимости а и со от параметров системы (т. с. для выбора параметров) целесообразнее применить другой путь решения задачи. Допусти.м, необходн.мо выбрать общий ко;)(к})иииснт усиле1шя k(k.Ji с учето.м влияния ра,зличных воз.чюжных значений постоянной Гд. Тогда, исключая kkrk из уравнений (18.156) и (18,157), находим

1 (1-ТоТ;Со2)?(а,со) + (7о + 7з)сог/(й,со)

а затем

k k k 2 (Го+т,)+Гд(1-7;,тУ)

Задаваясь теперь различны.ми зиачения.ми а и со и вычисляя каждый раз по этим фор.мулам 1\ и kkji/ получи.м сетку линий равных значений о) (о)]. щ,.,.) и а (а Oj, ...), показанных парне. 18.31, б. По этой диагра.м.ме удобно выбирать значения параметров kk-Ji/ и 1\ для получения желаемых а и со.

Кро.ме того, важными параметрами являются А к. и особенно м, и (см, рнс. 18.29). Но они входят в выражения qw q . Поэтому для опреде.теиия их влияния нужно построить графики q и q д.тя разных значений указа}1иых !1араметров, а затем, задаваясьз!!ачспиями а и сои используя соотношения (18.156) и (18.157), по потребным зиачешгям q и q определять эти параметры {и к, или к,). При этоуг нужно учитывать, что из требования вен1ествеппости выражений (18.151) и (18.152) следует выбирать

ut<--

т2 2 7, 0)

1

T.f(d +1

Пример 4. Рассмотрим систему автоматического управлепия с двумя нслн-пейпостя.ми в случае, когда их гармоническая линеаризация по отдельности певоз-

.можна вследствие отсут-

£2 Р

ствия свойства с)ильтра у звена, стоящего между ними (рис. 18.32).

Представим весь блок, вютючающий обе иелипейно-сти, изображеп1Н)1Й отдельно на рис. 18.33, как одно нелииейиое звепо. По отношению к нему система обладает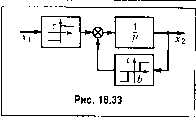

.г, =-{k2P + k)x,

рХ2 =

(18.158)

Чтобы пайти передаточную фу1И<:цию ьк)В010 нелинейного блока (рис. 18.33), оп-редели.м его выходной сигнал (/) при в.ходном сигпалех, = а s\u oit. Это представлено на рис. 18.34. Отсюда видно, что выходной сигнал Хо иредставляет собой ограниченные на уровне h треугольные колебания, отстаюпню но фа;зе от входного сигнала на угол Ф < п/2. Если вре.мя перехода выходного срп пала и.ч одного крайнего положения в другое составляет / , угол ф определяется соотнощением

ф = - 2 т/2

С учетом того, что / = 2h/c, Т

шЬ Ф = -.

271/со, гюлучае.м

(18.1,59)

Для того чтобы выходной си1нал достигал уровня ограниче1ШЯ (т. е. чтобы вторая нелинейность участвовала в работе), необходимо выполнение условия

71 со

Таким обрезом, следует рассматривать входные сиг-палы с частотой

со =

(18.160)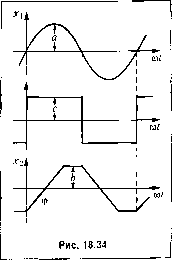

свойством фильтра. Следовательно, автоколеба1Н1я в системе можно искать приближенно в виде

= а sin со/.

Система уравнений, описывающих работу всей системы, имеет вид