Эквивалентная передаточная функция по ошибке (9.38)

7;лр+а;+7 м)/+1(1-т,/с)р

т,т,у+а\.+-1\,)р+р+к

Скоростная ошибка будет рав1Ш пулю в том случае, когда в числителе последнего выражения будет равен нулю коэффициент при операторе в первой степени. Отсюда получаем условие частичной инвариантности (ликвидация скоростной ошибки):

(9.41)

Из (9.39) можно найти эквивалентную передаточную функцию разомкнутой системы:

w;(p)=

К(\ + х,р)

р{\ + Т,р)(1 + Т р)-х,Кр

При выполнении условия (9.41) эквивалентная передаточная функция разомкнутой системы будет соответствовать астатизму второго порядка:

W,(p) =

К{\ + х,р)

К,{\ + х,р) (Ту+Т )р+ТуТ,У рЧ\+Т,р)

Т, + L,

у .4

- доброт1юсть систе.мы по ускорению, Г, =----эквивалент-

пая постоянная вре.мени.

В качестве BTopoio при.мера рассмотрим инер-циальную вертикать (рис. 9.13, а). Принцип работы ее заключается в том, что акселерометр А воспри1П1маетускоре1П!с перемешения подвижного объекта, на котором установлена стабилизированная платформа (СП), и составляющую ускорения силы тяжести, возникающую при наклоне этой платформ!.! на некоторый угол а (опгибка вертикали). Таким образом, акселерометр определяет ускорение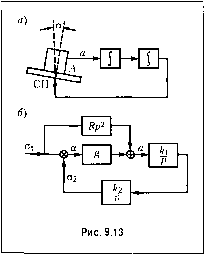

(9.42)

гдeg - ускорениесилы тяжести, R - радиус Земли, а, - путь, пройденный объектом по Земле, в дуговых единицах.

ф(Р) =

откуда следует, что должно быть выполнено равенство ,2 1/R- Тогда передаточная функция разомкнутой системы

Щр) = Щ{р)ШР>- (9.48)

а передаточная функция но ошибке будет тождественно равна нулю: Фхэ(р) 0. Следовательно, при любых движениях объекта, иа которо.м установлена инерциальная вертикаль, ошибка вертикали будет равна нулю. Это будет справедливым в том случае, если выполнены нулевые началыП)Ге условия, т. е. отсутствует свободное движение вертикали под действием начальных условии, и в случае, когда можно считать, что достаточно точно выполняется требуемое условие ,2 1/-

Замети.м, что в рассмотренно.м случае особенно важно иметь пулевые начальные условия вследствие того, что передаточной функции (9.48) соответствует характеристическое урапнепие

/+ = 0. (9.49)

R

Это ускорение дважды интегрируется и поступает на стабилизированную платформу, которая поворачивается на угол

k,k,

2=-а, (9 43)

где 1 и 2 ~ коэффициенты передачи первого и второго интеграторов.

К этим двум уравнениям необходимо добавить связь между ошибкой вертикали а, пройденны.м путем в дуговых единицах а, и угло.м поворота стабилизированной платформы

а = а, - 02. (9.44)

Для рассмотренных уравнений (9.42)-(9.44) инерциальной вертикали изобразим структурную схему (рис. 9,13, б). Сравнивая ее с рис. 9,11, можем записать:

Ф(р) V; (9.45)

W,{p)-g; (9.46)

W,ip)J-. (9.47)

Условие полной инвариантности (9.40)

Оно имеет чисто мнимые корни

Pi,2=±;J = ±;o

(9.50)

где Qo - частота незатухающих колебаний инерциальной вертикали, которой соответствует период Tq ~ 84,6 мин, называемый периодом Шулера. При наличии ненулевых начальных условий в систе.ме будут устанавливаться незатухающие колебания с частотой Qq, что будет нарушать работу вертикали.

Ко.мбипированное управление может быть использовано также для снижения ошибки от возмущаюпюго воздействия (рис. 9.14). В этом случае наряду с управлением по отклонению x(t) используется управление по возмущаюпюму воздействию f(t). Передаточная функция по воз.мущепию здесь будет иметь вид

ф/(р)=-

Wr{p)-ip(p)W(p)

W(p)

(9.51)

где Wj-(p) - передаточная функция поданному воз.мун1ению в разомкнутой системе, W(p) - передаточная функция разомкнутой системы.

Условие полной инвариантности может быть получено, если положить ФДр) = 0. Тогда

, л щ(р) W(p)

(9.,52)

Эта функция также может быть представлена в виде ряда аналогично формуле (9.36):

Ф(р) = /(ао +TiP + T/ +т1р + ...),

(9.53)

где йо - безразмерное число (1 или 0), ak - некоторый коэффициент, размерность которого совпадает с размерностью передаточной функции Wjip).

Как и в случае использования управления по задающему воздействию, получение полной инвариантности затрудняется необходимостью вводить первую и более высокие производные от воз.мущепия f{t). Поэтому используется, как правило, частичная инвариантность, получающаяся при реаш-зации в системе первых членов разложения (9.53). Это в свою очередь дает обранюние в нуль соответствующих первых коэффициентов ошибки но воз.мущепию (Cq, с С2 и т. д.).

В заключение за.мети.м, что возможно использование комбинированных систе.м с введепне.м управления по нескольким воз.мущающим во.здействиям и получением полной или частичной ннвариантно-сти по каждому из них. Одгшко это приводит, конечно, к усложнению схемы.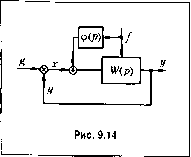